Chủ nhật, ngày 01/12/2024, 06:12 (GMT +7)
ĐỀ CƯƠNG VÀ MA TRẬN ÔN TẬP HỌC KÌ I MÔN TOÁN LỚP 11 NĂM HỌC 2024-2025
Đây là đề cương và ma trận toán lớp 11 chính thức của trường Trường THPT Nguyễn Gia Thiều trong năm học 2024 – 2025. Đề kiểm tra, đáp án và ma trận đặc tả sẽ được cập nhật ngay sau khi kiểm tra xong.
Nội dung yêu cầu cụ thể theo ma trận đề kiểm tra.
|
Dạng thức |
Câu | Năng lực toán học |
| |||||||||
| Tư duy và lập luận toán học (TD) | Giải quyết vấn đề toán học (GQ) | Mô hình hóa toán học (MH) |
Chủ đề, nội dung môn học | |||||||||
| Cấp độ tư duy | Cấp độ tư duy | Cấp độ tư duy | ||||||||||
| Biết | Hiểu | VD | Biết | Hiểu | VD | Biết | Hiểu | VD |
| |||
| 1 | 1 | * |
|
|
|
|
|
|
|
|
| |
| 2 | * |
|
|
|
|
|
|
|
|
| ||
| 3 | * |
|
|
|
|
|
|
|
|
| ||
| 4 | * |
|
|
|
|
|
|
|
|
| ||
| 5 | * |
|
|
|
|
|
|
|
|
| ||
| 6 | * |
|
|
|
|
|
|
|
|
| ||
| 7 | * |
|
|
|
|
|
|
|
|
| ||
| 8 | * |
|
|
|
|
|
|
|
|
| ||
| 9 |
| * |
|
|
|
|
|
|
|
| ||
| 10 |
| * |
|
|
|
|
|
|
|
| ||
| 11 |
|
|
|
| * |
|
|
|
|
| ||
| 12 |
|
|
|
|
|
|
| * |
|
| ||
| T K | 8 | 2 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| ||
| 2 |
1 | a | * |
|
|
|
|
|
|
|
|
|
| b | * |
|
|
|
|
|
|
|
|
| ||
| c | * |
|
|
|
|
|
|
|
|
| ||
| d |
| * |
|
|
|
|
|
|
|
| ||
|
2 | a | * |
|
|
|
|
|
|
|
|
| |
| b | * |
|
|
|
|
|
|
|
|
| ||
| c | * |
|
|
|
|
|
|
|
|
| ||
| d | * |
|
|
|
|
|
|
|
|
| ||
|
3 | a |
|
|
| * |
|
|
|
|
|
| |
| b |
|
|
| * |
|
|
|
|
|
| ||
| c |
|
|
|
| * |
|
|
|
|
| ||
| d |
|
|
|
|
| * |
|
|
|
| ||
|
4 | a |
|
|
|
|
|
| * |
|
|
| |
| b |
|
|
|
|
|
| * |
|
|
| ||
| c |
|
|
|
|
|
|
| * |
|
| ||
| d |
|
|
|
|
|
|
| * |
|
| ||
| T | K | 7 | 1 | 0 | 2 | 1 | 1 | 2 | 2 | 0 |
| |
| 3 | 1 |
| * |
|
|
|
|
|
|
|
| |
| 2 |
| * |
|
|
|
|
|
|
|
| ||
| 3 |
|
|
|
|
|
| * |
|
|
| ||
| 4 |
|
|
|
| * |
|
|
|
|
| ||
| 5 |
|
| * |
|
|
|
|
|
|
| ||
| 6 |
|
|
|
|
|
|
|
| * |
| ||
| T K | 0 | 2 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| ||
CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC (cả chương)
CHƯƠNG II. DÃY SỐ. CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN (cả chương)
CHƯƠNG III. GIỚI HẠN. HÀM SỐ LIÊN TỤC (từ đầu chương đến hết bài 2: Giới hạn của hàm số)
CHƯƠNG IV. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG (từ đầu chương đến hết bài 4: Hai mặt phẳng song song).
Câu 1. Cho hình vẽ bên, số đo của góc lượng giác $\left( OA,OM \right)$ là
A. ${{30}^{o}}+k{{360}^{o}},k\in \mathbb{Z}.$
B. ${{150}^{o}}+k{{360}^{o}},k\in \mathbb{Z}.$
C. $-{{150}^{o}}+k{{360}^{o}},k\in \mathbb{Z}.$
D. $-{{30}^{o}}+k{{360}^{o}},k\in \mathbb{Z}.$
Câu 2. Một chiếc đồng hồ, có kim chỉ giờ ${{OG}}$ chỉ số 9 và kim phút ${{OP}}$ chỉ số 12. Số đo của góc lượng giác $\left( OG,OP \right)$ là
A. $\dfrac{\pi }{2}+k2\pi ,\,\,k\in \mathbb{Z}$.
B. $-\,{{270}^{0}}+k{{360}^{0}},\,\,k\in \mathbb{Z}.$
C. ${{270}^{0}}+k{{360}^{0}},\,\,k\in \mathbb{Z}$.
D. $\dfrac{9\pi }{10}+k2\pi ,\,\,k\in \mathbb{Z}$.
Câu 3. Biểu thức $\dfrac{\cos \left( 2024\pi -x \right)\,\,\,\,+\,\,\,\,\sin \left( \pi -x \right)\,\,\,\,-\,\,\,\,2.\cos \pi }{2.\tan \dfrac{\pi }{4}+\sin \left( \dfrac{\pi }{2}-x \right)+\sin \left( \pi +x \right)-2.\cos \left( \dfrac{\pi }{2}+x \right)}$ có giá trị bằng
A. 0. B. 1. C. $\cos x$. D. $\sin x$.
Câu 4. Biểu thức ${{\left[ \sin \left( \dfrac{\pi }{2}-x \right)+\sin \left( 10\pi +x \right) \right]}^{2}}+{{\left[ \cos \left( \dfrac{3\pi }{2}-x \right)+\cos \left( 8\pi -x \right) \right]}^{2}}$ có giá trị bằng
A. $\dfrac{1}{2}.$ B. $\dfrac{3}{4}.$ C. 1. D. 2.
Câu 5. Rút gọn $M=\cos \left( x+\dfrac{\pi }{4} \right)-\cos \left( x-\dfrac{\pi }{4} \right)$ ta được
A. $M=-\sqrt{2}\sin x.$ B. $M=-\sqrt{2}\cos x.$ C. $M=\sqrt{2}\sin x.$ D. $M=\sqrt{2}\cos x.$
Câu 6. Cho biểu thức $P=\cos 2x+a.{{\sin }^{2}}x$. Số thực $a$ để $P$ không phụ thuộc vào biến $x$ là
A. $a=-2$. B. $a=-1$. C. $a=1$. D. $a=2$.
Câu 7. Hàm số $y=\sin x$ tuần hoàn với chu kỳ bằng
A. $\pi $. B. $2\pi $. C. $3\pi $. D. $4\pi $.
Câu 8. Khẳng định nào dưới đây là sai ?
A. Hàm số ${y=\cos x}$ là hàm số lẻ. B. Hàm số ${y=\cot x}$ là hàm số lẻ.
C. Hàm số ${y=\sin x}$ là hàm số lẻ. D. Hàm số ${y=\tan x}$ là hàm số lẻ.
Câu 9. Hàm số $y=\sin 7x$ có tập giá trị là
A. $T=\mathbb{R}$. B. $T=\left[ -1;1 \right]$. C. $T=\left[ -7;7 \right]$. D. $T=\left( 7;+\infty \right)$.
Câu 10. Hàm số ${y=\sin x}$ đồng biến trên khoảng nào trong các khoảng sau
A. ${\left( -\dfrac{\pi }{2};\dfrac{\pi }{2} \right)}$. B. ${\left( 0;\pi \right)}$. C. ${\left( 0;2\pi \right)}$. D. ${\left( \dfrac{\pi }{2};\pi \right)}$.
Câu 11. Cho dãy số $\left( {{u}_{n}} \right)$ được xác định bởi ${{u}_{1}}=1$ và ${{u}_{n+1}}=2{{u}_{n}}-5$ với mọi $n\in {{\mathbb{N}}^{*}}$. Số hạng ${{u}_{3}}$ bằng
A. ${-5}$. B. ${-11}$. C. ${-3}$. D. ${-1}$.
Câu 12. Cho dãy số $\left( {{u}_{n}} \right),$ biết ${{u}_{n}}=\dfrac{2n+5}{5n-4}.$ Số $\dfrac{7}{12}$ là số hạng thứ mấy của dãy số ?
A. 6. B. 8. C. 9. D. 10.
Câu 13. Trong các dãy số sau, dãy số tăng là
A. $1;\text{ }1;\text{ }1;\text{ }1;\text{ }1;\text{ }1;\cdots$
B. $1;\text{ }-\dfrac{1}{2};\text{ }\dfrac{1}{4};\text{ }-\dfrac{1}{8};\text{ }\dfrac{1}{16};\cdots$
C. $1;\text{ }3;\text{ }5;\text{ }7;\text{ }9;\cdots$
D. $1;\text{ }\dfrac{1}{2};\text{ }\dfrac{1}{4};\text{ }\dfrac{1}{8};\text{ }\dfrac{1}{16};\cdots$
Câu 14. Trong các dãy số ${\left( {{u}_{n}} \right)}$ cho bởi số hạng tổng quát ${{{u}_{n}}}$ sau, dãy số nào là dãy số giảm ?
A. ${{{u}_{n}}=\dfrac{1}{{{2}^{n}}}.}$ B. ${{{u}_{n}}=\dfrac{3n-1}{n+1}.}$ C. ${{{u}_{n}}={{n}^{2}}.}$ D. ${{{u}_{n}}=\sqrt{n+2}.}$
Câu 15. Cho dãy số ${\left( {{u}_{n}} \right)}$, biết ${{{u}_{n}}=\dfrac{3n-1}{3n+1}}$. Dãy số ${\left( {{u}_{n}} \right)}$ bị chặn trên bởi số
A. 0. B. ${\dfrac{1}{3}.}$ C. ${\dfrac{1}{2}.}$ D. 1.
Câu 16. Cho cấp số cộng $\left( {{u}_{n}} \right)$ với ${{u}_{n}}=3n-7$. Số hạng đầu ${{u}_{1}}$ và công sai $d$ của cấp số cộng này là
A. ${{u}_{1}}=-4;d=3.$ B. ${{u}_{1}}=4;d=3.$ C. ${{u}_{1}}=-4;d=-3.$ D. ${{u}_{1}}=4;d=-3.$
Câu 17. Cho cấp số cộng ${\left( {{u}_{n}} \right)}$ có số hạng đầu ${{u}_{1}}=-\dfrac{1}{2},$ công sai $d=\dfrac{1}{2}.$ Năm số hạng liên tiếp đầu tiên của cấp số cộng là
A. $-\dfrac{1}{2};0;1;\dfrac{1}{2};1.$ B. $-\dfrac{1}{2};0;\dfrac{1}{2};0;\dfrac{1}{2}.$ C. $\dfrac{1}{2};1;\dfrac{3}{2};2;\dfrac{5}{2}.$ D. $-\dfrac{1}{2};0;\dfrac{1}{2};1;\dfrac{3}{2}.$
Câu 18. Cho cấp số cộng $\left( {{u}_{n}} \right)$ có các số hạng đầu lần lượt là $5;\,\text{ }9;\text{ }\,13;\,\text{ }17;\text{ }\cdots$. Số hạng tổng quát ${{u}_{n}}$ của cấp số cộng là
A. ${{u}_{n}}=5n+1.$ B. ${{u}_{n}}=5n-1.$ C. ${{u}_{n}}=4n+1.$ D. ${{u}_{n}}=4n-1.$
Câu 19. Cho cấp số cộng ${\left( {{u}_{n}} \right)}$ có ${{{u}_{1}}=\dfrac{1}{4}}$ và ${d=-\dfrac{1}{4}.}$ Gọi ${{S}_{5}}$ là tổng $5$ số hạng đầu tiên của cấp số cộng đã cho, khi đó
A. ${{{S}_{5}}=-\dfrac{5}{4}.}$ B. ${{{S}_{5}}=\dfrac{4}{5}.}$ C. ${{{S}_{5}}=\dfrac{5}{4}.}$ D. ${{{S}_{5}}=-\dfrac{4}{5}.}$
Câu 20. Người ta trồng 3003 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây . . . Số hàng cây trồng là
A. 73. B. 75. C. 77. D. 78.
Câu 21. Một cấp số nhân có hai số hạng liên tiếp là 16 và 36. Số hạng tiếp theo là
A. 720. B. 81. C. 64. D. 56.
Câu 22. Trong các dãy số sau, dãy số nào là một cấp số nhân ?
A. ${-3\,;\ -6\,;\ -12\,;\ 24}$. B. ${-3\,;\ 6\,;\ -12\,;\ -24}$. C. ${3\,;\ 6\,;\ -12\,;\ -24}$. D. ${3\,;\ -6\,;\ 12\,;\ -24}$.
Câu 23. Cấp số nhân $\left( {{u}_{n}} \right)$ có số hạng tổng quát là ${{u}_{n}}=\dfrac{3}{5}{{.2}^{n-1}},n\in {{\mathbb{N}}^{*}}$. Số hạng đầu tiên và công bội của cấp số nhân đó là
A. ${{{u}_{1}}=\dfrac{6}{5},q=2}$. B. ${{{u}_{1}}=\dfrac{3}{5},q=-2}$. C. ${{{u}_{1}}=\dfrac{6}{5},q=-2}$. D. ${{{u}_{1}}=\dfrac{3}{5},q=2}$.
Câu 24. Cho cấp số nhân ${\left( {{u}_{n}} \right)}$ có ${{{u}_{1}}=-1}$ và ${q=-\dfrac{1}{10}}$. Số ${\dfrac{1}{{{10}^{103}}}}$ là số hạng thứ mấy của cấp số nhân đã cho ?
A. Số hạng thứ 103. B. Số hạng thứ 104. C. Số hạng thứ 105. D. Số hạng thứ 106.
Câu 25. Cho cấp số nhân ${\left( {{u}_{n}} \right)}$ có ${{{u}_{1}}=-3}$ và ${q=-2.}$ Tổng 10 số hạng đầu tiên của cấp số nhân đã cho là
A. ${{S}_{10}}=-511.$ B. ${{S}_{10}}=-1025.$ C. ${{S}_{10}}=1025.$ D. ${{S}_{10}}=1023.$
Câu 26. Một cơ sở khoan giếng đưa ra mức giá như sau: Giá từ mét khoan đầu tiên là 100 000 đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm 30 000 đồng so với giá của mét khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan giếng sâu 20 mét lấy nước dùng cho tưới tiêu cây trồng. Số tiền khoan giếng là
A. 8800000 đồng. B. 7700000 đồng. C. 9980000 đồng. D. 6670000 đồng.
Câu 27. Chiều cao (đơn vị: centimét) của một đứa trẻ $n$ tuổi phát triển bình thường được cho bởi công thức: ${{x}_{n}}=75+5\left( n-1 \right)$ (Nguồn: https:///bibabo.vn). Trung bình một năm, chiều cao mỗi đứa trẻ phát triển bình thường tăng lên
A. 5 centimét. B. 7 centimét. C. 10 centimét. D. 16 centimét.
Câu 28. Một gia đình mua một chiếc ô tô điện giá 999 triệu đồng. Trong điều kiện sử dụng bình thường (không chạy dịch vụ, không chở hàng nhiều, không tai nạn nặng, không ngập nước …) trung bình mỗi năm, giá trị còn lại của ô tô giảm đi 10% (so với năm trước đó). Sau 6 năm sử dụng, giá trị của ô tô ước tính không vượt quá bao nhiêu triệu đồng (làm tròn đến hàng triệu đồng) ?
A. 530 triệu. B. 531 triệu. C. 589 triệu. D. 590 triệu.
Câu 29. Ông X gửi 850 triệu đồng tiết kiệm vào một ngân hàng với lãi suất 6%/năm với kì hạn 2 năm, theo thể thức lãi kép (nghĩa là lãi năm trước nhập vào gốc của năm tiếp theo). Sau 2 năm ông X rút tiền cả gốc và lãi ước tính được (làm tròn đến hàng triệu đồng)
A. 955 triệu. B. 954 triệu. C. 901 triệu. D. 900 triệu.
Câu 30. Một công ty điện lực đề xuất giá bán điện sinh hoạt cho nhà ông An theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 50 số điện (với 1 số điện bằng 1 kWh): bậc một từ số điện thứ 1 đến số điện thứ 50; bậc hai từ số điện thứ 51 đến số điện thứ 100; ... Giá của mỗi số điện ở bậc 1 là 1800 đồng, kể từ bậc 2 trở đi mỗi số điện tăng hơn 4% so với giá của mỗi số điện ở bậc kế trước. Tháng vừa qua nhà ông An dùng hết 610 số điện, số tiền điện ông An phải trả (làm tròn đến hàng nghìn đồng) là
A. 1 381 000 đồng. B. 1 300 000 đồng. C. 1 271 000 đồng. D. 1 204 000 đồng.
Câu 31. Tổng $S=1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...$ bằng
A. 1. B. 2. C. $\dfrac{2}{3}$. D. $\dfrac{3}{2}$.
Câu 32. ${\lim \dfrac{2}{n-3}}$ bằng
A. +∞. B. 2. C. ${-\dfrac{2}{3}}$. D. 0.
Câu 33. $\lim \dfrac{2n+3}{n-1}$ bằng
A. 1. B. $-\dfrac{3}{2}$. C. $-3$. D. 2.
Câu 34. $\lim \left( -{{n}^{3}}+2n+3 \right)$ bằng
A. $-\infty$. B. $+\infty$. C. 1. D. $-1$.
Câu 35. $\underset{{}}{\mathop{\lim }}\,\dfrac{{{2}^{n}}-{{3}^{n}}}{{{2}^{n}}+1}$ bằng
A. $-\infty$. B. $0$. C. $+\infty$. D. $\dfrac{3}{2}$.
Câu 36. $\underset{x\to -2}{\mathop{\lim }}\,\dfrac{2{{x}^{2}}+3x-2}{{{x}^{2}}-4}$ bằng
A. $\dfrac{5}{4}$. B. $-\dfrac{5}{4}$. C. $\dfrac{1}{4}$. D. 2.
Câu 37. $\underset{x\to -\infty }{\mathop{\lim }}\,\dfrac{2x+1}{x+1}$ bằng
A. $\dfrac{1}{2}$. B. 1. C. 2. D. $-1$.
Câu 38. $\underset{x\to {{2}^{+}}}{\mathop{\lim }}\,\dfrac{\sqrt{x+2}}{\sqrt{x-2}}$ bằng
A. $-\infty .$ B. $+\infty .$ C. $-\dfrac{15}{2}.$ D. 0.
Câu 39. Yếu tố nào sau đây xác định một mặt phẳng duy nhất ?
A. Ba điểm phân biệt. B. Một điểm và một đường thẳng.
C. Hai đường thẳng cắt nhau. D. Bốn điểm phân biệt.
Câu 40. Cho hai đường thẳng song song ${a}$ và ${b}$. Có bao nhiêu mặt phẳng chứa ${a}$ và song song với ${b}$ ?
A. Một mặt phẳng. B. Hai mặt phẳng. C. Vô số mặt phẳng. D. Không có mặt phẳng nào.
Câu 41. Khẳng định nào dưới đây đúng ?
A. Hai đường thẳng không có điểm chung thì chéo nhau.
B. Hai đường thẳng phân biệt không song song thì chéo nhau.
B. Hai đường thẳng nằm trên hai mặt phẳng phân biệt thì chéo nhau.
D. Hai đường thẳng song song thì không có điểm chung.
Câu 42. Trong không gian, cho ba đường thẳng $a,\,\,b,\,\,c$. Trong các khẳng định sau, khẳng định nào đúng ?
A. Nếu ${a}$ và ${b}$ không cắt nhau thì ${a}$ và ${b}$ song song.
B. Nếu ${b}$ và ${c}$ chéo nhau thì ${b}$ và ${c}$ không cùng thuộc một mặt phẳng.
C. Nếu ${a}$ và ${b}$ cùng chéo nhau với ${c}$ thì ${a}$ song song với ${b}$.
D. Nếu ${a}$ và ${b}$ cắt nhau, ${b}$ và ${c}$ cắt nhau thì ${a}$ và ${c}$ cắt nhau.
Câu 43. Cho hình chóp ${S.ABCD}$ có đáy ${ABCD}$ là hình bình hành. Trong các cặp đường thẳng sau, cặp đường thẳng nào cắt nhau ?
A. ${AB}$ và ${CD}$. B. ${AC}$ và ${BD}$. C. ${SB}$ và ${CD}$. D. ${SD}$ và ${BC}$.
Câu 44. Cho đường thẳng ${a}$ song song với mặt phẳng ${(\alpha)}$. Nếu mặt phẳng ${(\beta)}$ chứa ${a}$ và cắt ${(\alpha)}$ theo giao tuyến ${b}$ thì ${b}$ và ${a}$ là hai đường thẳng
A. Cắt nhau. B. Trùng nhau. C. Chéo nhau. D. Song song với nhau.
Câu 45. Cho hình chóp ${S.ABCD}$ đáy ${ABCD}$ là hình bình hành tâm $O$. Gọi $M$ là trung điểm của ${SB}$. Giao điểm của ${DM}$ và $\left( SAC \right)$ là
A. giao điểm của ${DM}$ và ${SA}$. B. giao điểm của ${DM}$ và ${SC}$.
C. giao điểm của ${DM}$ và ${SO}$. D. giao điểm của ${DM}$ và $AC$.
Câu 46. Cho hình chóp ${S.ABCD}$. Gọi $M$ và $N$ lần lượt là trung điểm của ${SA}$ và ${SC}$. Khẳng định nào sau đây đúng ?
A. $MN\text{//}\left( ABCD \right)$. B. $MN\text{//}\left( SAB \right)$. C. $MN\text{//}\left( SCD \right)$. D. $MN\text{//}\left( SBC \right)$.
Câu 47. Cho hình chóp ${S.ABCD}$, có đáy ${ABCD}$ là hình bình hành ${M}$ là trung điểm của cạnh ${BC}$, $I$ thuộc cạnh ${SC}$ sao cho $SI=2IC$, $P$ là giao điểm của ${AC}$ với $\left( SMD \right)$ và $H$ là giao điểm của ${SD}$ với $\left( AIM \right)$ (tham khảo hình vẽ). Ta có
 A. $IP\,\,//\,\,\left( SAD \right)$. B. $IP\,\,//\,\,\left( SBD \right)$. C. $IA\,\,//\,\,\left( SBD \right)$. D. $\dfrac{SH}{SD}\,\,=\,\,\dfrac{1}{3}$.
A. $IP\,\,//\,\,\left( SAD \right)$. B. $IP\,\,//\,\,\left( SBD \right)$. C. $IA\,\,//\,\,\left( SBD \right)$. D. $\dfrac{SH}{SD}\,\,=\,\,\dfrac{1}{3}$.
Câu 48. Cho hai mặt phẳng phân biệt $\left( P \right)$ và $\left( Q \right)$; đường thẳng $a\subset \left( P \right),\,\,b\subset \left( Q \right)$. Khẳng định sai là
A. Nếu $\left( P \right)//\left( Q \right)$ thì $a//b$.
B. Nếu $\left( P \right)//\left( Q \right)$ thì $b//\left( P \right)$.
C. Nếu $\left( P \right)//\left( Q \right)$ thì $a$ và $b$ hoặc song song hoặc chéo nhau.
D. Nếu $\left( P \right)//\left( Q \right)$ thì $a//\left( Q \right)$.
Câu 49. Cho hình chóp ${S.ABCD}$, có đáy ${ABCD}$ là hình bình hành tâm $O$. Gọi ${M,N}$ lần lượt là trung điểm ${SA,SD}$. Mặt phẳng $\left( OMN \right)$ song song với mặt phẳng
A. $\left( SBC \right)$. B. $\left( SCD \right)$. C. $\left( ABCD \right)$. D. $\left( SAB \right)$.
Câu 50. Cho hình chóp ${S.ABCD}$ có đáy ${ABCD}$ là hình bình hành tâm ${O}$. Gọi ${M}$, ${N}$, $P$ theo thứ tự là trung điểm của ${SA}$, ${SD}$ và ${AB}$. Khi đó
A. $\left( NMP \right)\ \text{//}\ \left( SBD \right)$. B. $\left( NOM \right)$ cắt ${\left( OPM \right)}$.
C. ${\left( MON \right)\ \text{//}\ \left( SBC \right)}$. D. $\left( PON \right)\cap \left( MNP \right)=NP$.
Câu 51. Cho hình chóp ${S . A B C D}$ có đáy ${A B C D}$ là hình bình hành tâm ${O}$, gọi ${M, N}$ lần lượt là trung điểm của ${S A, S D}$. Khi đó
A. ${ON}$ và ${SB}$ cắt nhau. B. $\left( OMN \right)\,\,//\,\,\left( SBC \right)$.
C. $\left( OMN \right)$ cắt $\left( SBC \right)$. D. ${SB}$ cắt $\left( OMN \right)$.
Câu 52. Cho hình chóp ${S . A B C D}$ có đáy là hình thang với ${A D}$ là đáy lớn và ${A D=2 B C}$. Gọi ${M, N}$ theo thứ tự là trung điểm của ${S A}$ và ${A D}$. Khẳng định sai là
A. $MN\,\,//\,\,\left( SCD \right)$. B. $CD\,\,//\,\,\left( BMN \right)$.
C. $\left( BMN \right)\,\,//\,\,\left( SCD \right)$. D. $\left( BMN \right)$ cắt $\left( SCD \right)$.
Câu 53. Cho hình chóp ${S . A B C D}$, đáy ${A B C D}$ là hình bình hành có ${O}$ là giao điểm của hai đường chéo. Gọi ${M, N}$ lần lượt là trung điểm của $SA,\,\,SD$. Gọi ${E}$ là trung điểm của ${A B}$, ${F}$ là một điểm thuộc ${O N}$. Khẳng định sai là
A. $OM\,\,//\,\,SC$. B. $SB\,\,//\,\,\left( OMN \right)$. C. $\left( OMN \right)\,\,//\,\,\left( SBC \right)$. D. ${FE}$ cắt $\left( SBC \right)$.
Câu 54. Cho hình chóp ${S.ABCD}$ có đáy ${ABCD}$ là hình thang đáy ${AD}$ và ${BC}$. Gọi $M$ là trọng tâm tam giác ${SAD}$, $N$ là điểm thuộc đoạn ${AC}$ sao cho ${NA=\dfrac{NC}{2}}$, $P$ là điểm thuộc đoạn ${CD}$ sao cho ${PD=\dfrac{PC}{2}.}$ Khi đó
A. Giao tuyến của hai mặt phẳng $\left( SBC \right)$ và $\left( MNP \right)$ song song với ${BC}$.
B. ${MN}$ cắt $\left( SBC \right)$.
C. $MN\text{//}\left( SBC \right)$ và $\left( MNP \right)\text{//}\left( SBC \right)$.
D. $\left( MNP \right)\text{//}\left( SAD \right)$.
Câu 55. Cho hình chóp ${S.ABCD}$ đáy là hình thang, ${AB//CD,}$$AB=a;$$CD=2a$, gọi ${I}$ là giao điểm của ${AC}$ và ${BD.}$ Qua ${I}$ kẻ đường thẳng song song ${CD}$ cắt ${BC}$ tại ${M.}$ Trên cạnh ${SC}$ lấy điểm ${N}$ sao cho $CN=2NS$ (tham khảo hình vẽ). Khi đó
A. $\left( IMN \right)\,\text{//}\,\left( SAB \right)$. B. $\left( IMN \right)\,\text{//}\,\left( SAD \right)$. C. $\left( IMN \right)\,\text{//}\,\left( SAC \right)$. D. $\left( IMN \right)\,\text{//}\,\left( SBD \right)$.
Câu 56. Với mọi số thực ${x}$.
a) ${\sin x=\sin (-x).}$
b) ${\sin (\pi -x)=\sin x.}$
c) $\cos x=\sin \left( \dfrac{\pi }{2}-x \right)$.
d) ${\tan x=\tan (\pi +x).}$
Câu 57. Cho phương trình ${\sin \left(2 x-\dfrac{\pi}{4}\right)=\sin \left(x+\dfrac{3 \pi}{4}\right)}$.
a) Phương trình có nghiệm $\left[ \begin{array}{*{35}{l}} x=\pi +k2\pi \\ x=\dfrac{\pi}{6}+k\dfrac{2\pi }{3} \\\end{array}\,\,(k\in \mathbb{Z}) \right.$.
b) Trong khoảng $(0;\pi )$ phương trình có 2 nghiệm.
c) Tổng các nghiệm của phương trình trong khoảng $(0;\pi )$ bằng $\dfrac{7\pi }{6}$.
d) Trong khoảng $(0;\pi )$ phương trình có nghiệm lớn nhất bằng $x=\dfrac{\pi }{6}$.
Câu 58. Cho cấp số cộng $\left( {{u}_{n}} \right)$ có số hạng đầu ${{u}_{1}}=\dfrac{3}{2}$, công sai $d=\dfrac{1}{2}$.
a) Số hạng tổng quát là ${{u}_{n}}=1+\dfrac{n}{3}$.
b) 5 là số hạng thứ 8 của cấp số cộng đã cho.
c) $\dfrac{15}{4}$ là một số hạng của cấp số cộng đã cho.
d) Tổng 100 số hạng đầu của cấp số cộng $\left( {{u}_{n}} \right)$ bằng 2620.
Câu 59. Các nhà môi trường phát hiện một chủng vi khuẩn mới. Kể từ lúc phát hiện đến thời điểm t (giờ) số lượng vi khuẩn được các nhà môi trường mô tả bởi công thức ${u\left( t \right)=\dfrac{at+6}{t+3}}$, (${a>2}$) (nghìn tế bào).
a) Số lượng vi khuẩn ban đầu là 2 (nghìn tế bào).
b) Sau 3 giờ người ta thấy có 51 nghìn tế bào vi khuẩn, khi đó ${a<50}$.
c) Nếu xem $\left( {{u}_{t}} \right)$, $t\in \mathbb{N}^*$ là một dãy số với $u(t)=\dfrac{at+6}{t+3},\,\,a>2$ thì dãy số $\left( {{u}_{t}} \right)$ là dãy số tăng.
d) Nếu số lượng vi khuẩn luôn tăng theo thời gian nhưng không vượt quá 100 nghìn tế bào thì ${a\le 100}$.
Câu 60. Cho hàm số $y=f\left( x \right)=\dfrac{a{{x}^{2}}+bx+c}{{{x}^{2}}-x}$.
a) Nếu $a=1,b=-1,c=0$ thì $\underset{x\to 1}{\mathop{\lim }}\,f\left( x \right)=1$.
b) Nếu $\underset{x\to +\infty }{\mathop{\lim }}\,f\left( x \right)=2$ thì $a=2$.
c) Nếu $\underset{x\to 0}{\mathop{\lim }}\,f\left( x \right)$ có giới hạn hữu hạn thì $c=0$.
d) Nếu $\underset{x\to 1}{\mathop{\lim }}\,f\left( x \right)$ có giới hạn hữu hạn và $\underset{x\to 0}{\mathop{\lim }}\,f\left( x \right)=3$ thì $a+2b+3c=0$.
Câu 61. Aladin nhặt được cây đèn thần, chàng miết tay vào cây đèn và gọi Thần đèn ra. Thần đèn cho chàng 3 điều ước. Aladin ước 2 điều đầu tiên tùy thích, nhưng điều ước thứ 3 của chàng là: "Ước gì ngày mai tôi lại nhặt được cây đèn và Thần cho tôi số điều ước gấp đôi số điều ước ngày hôm nay". Thần đèn chấp thuận và mỗi ngày Aladin đều thực hiện theo quy tắc như trên: ước hết các điều đầu tiên và luôn chừa lại điều ước cuối cùng để kéo dài thỏa thuận với thần đèn cho ngày hôm sau.
a) Ngày thứ hai Aladin ước 6 điều.
b) Ngày thứ ba Aladin ước 12 điều.
c) Ngày thứ tư Aladin ước 48 điều.
d) Sau hai tuần gặp Thần đèn, Aladin ước tất cả 49 149 điều ước.
Câu 62. Anh X kí hợp đồng lao động trong 5 năm với điều khoản về tiền lương như sau: Tháng đầu tiên, tiền lương của anh X là 26 triệu. Kể từ tháng thứ tư trở đi, cứ sau ba tháng một lần tiền lương của anh được tăng lên 4% so với tháng trước.
a) Tháng thứ tư kể từ ngày đi làm anh X được lương trên 27 triệu.
b) Tổng tiền lương anh X nhận được trong 12 tháng đầu tiên đi làm là hơn 331 triệu.
c) Hàng tháng anh X tiết kiệm vào tài khoản đúng bằng 20% tiền lương của tháng đó, biết lãi suất trong tài khoản nhỏ như không có. Tổng tiền tiết kiệm trong 2 năm đầu là hơn 144 triệu.
d) Hàng tháng anh X tiết kiệm vào tài khoản đúng bằng 20% tiền lương của tháng đó, biết lãi suất trong tài khoản nhỏ như không có. Anh X cần 19 tháng tiết kiệm lương sẽ đủ để mua chiếc xe máy giá 150 triệu.
Câu 63. Cho hình chóp ${S.ABCD}$ có đáy là hình bình hành. Qua $S$ kẻ $Sx;\,\,Sy$ lần lượt song song với $AB,\,\,AD$.
a) Giao tuyến của $\left( SAC \right)$ và $\left( SBD \right)$ là đường thẳng ${Sx}$.
b) Giao tuyến của $\left( SBD \right)$ và $\left( SAC \right)$ là đường thẳng ${Sy}$.
c) Giao tuyến của $\left( SAB \right)$ và $\left( SCD \right)$ là đường thẳng ${Sx}$.
d) Giao tuyến của $\left( SAD \right)$ và $\left( SBC \right)$ là đường thẳng ${Sx}$.
Câu 64. Cho hình chóp ${S.ABCD}$ có đáy là hình thang đáy lớn là ${CD}$. Gọi $M$ là trung điểm của ${SA}$, $N$ là giao điểm của ${SB}$ và mặt phẳng $\left( MCD \right)$.
a) ${MN}$ và ${SD}$ cắt nhau.
b) ${MN}$ và ${AB}$ cắt nhau.
c) ${MN}$ và $SC$ cắt nhau.
d) $MN\,\,//\,\,CD$.
Câu 65. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Mặt phẳng $\left( P \right)$ cắt các cạnh $SA$, $SB$, $SC$, $SD$ lần lượt tại ${M}$, $N$, $P$, $Q$ . Gọi $I$ là giao điểm của $MQ$ và $NP$.
a) $SI\text{//}AB$.
b) $SI\text{//}AC$.
c) $SI\text{//}AD$.
d) $SI\text{//}BD$.
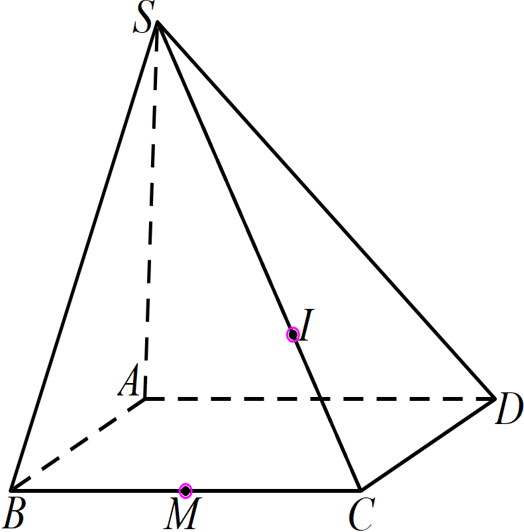
Câu 66. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $O$ là giao điểm của $AC$ và $BD$, $G$ là trọng tâm tam giác $ABC$, $M$ là trung điểm cạnh $SC$. Gọi $I$ là giao điểm của $AM$ với $\left( SBD \right)$, $K$ là giao điểm của $SD$ với mặt phẳng ${\left( AGM \right)}$ (tham khảo hình vẽ).
a) $I$ cũng là giao điểm của $AM$ với $SO$.
b) $IG\,\,//\,\,\left( SAD \right)$.
c) $AG$, $CD$, $MK$ là ba đường thẳng đồng quy.
d) $\dfrac{SD}{SK}=\dfrac{3}{2}$.
Câu 67. Cho hình chóp ${S . A B C D}$ có đáy ${A B C D}$ là hình bình hành. Gọi ${H, I, K}$ lần lượt là trung điểm của ${S A, S B, S C}$. Gọi ${M}$ là giao điểm của ${A I}$ và ${K D, N}$ là giao điểm của ${D H}$ và ${C I}$.
a) $HI//(ABCD)$.
b) ${(H I K) / /(A B C D)}$.
c) ${SM}$ và ${HI}$ chéo nhau.
d) ${(S M N) / /(H I K)}$.
Câu 68. Cho hình chóp ${S . A B C D}$ có đáy là hình bình hành tâm ${O}$. Gọi ${M, N}$ lần lượt là trung điểm của ${S A}$ và ${S D}$.
a) ${M N / / A D \Rightarrow M N / / B C \Rightarrow M N / /(S B C)}$.
b) ${(O M N) / /(S B C)}$.
c) Gọi ${E}$ là trung điểm đoạn ${A B}$ và ${F}$ là một điểm thuộc đoạn ${O N}$. Khi đó ${E F}$ cắt với mặt phẳng ${(S B C)}$.
d) Gọi ${G}$ là một điểm trên mặt phẳng ${(A B C D)}$ cách đều ${A B}$ và ${C D}$. Khi đó ${GN}$ cắt ${G N / /(S A B)}$.
Câu 69. Cho hình bình hành ${A B C D}$ và ${A B E F}$ nằm ở hai mặt phẳng khác nhau. Gọi ${M}$ là trọng tâm ${\Delta A B E}$. Gọi ${(P)}$ là mặt phẳng đi qua ${M}$ và song song với mặt ${(A D F)}$. Lấy ${N}$ là giao điểm của ${(P)}$ và ${A C}$.
a) ${EFDC}$ là hình thang.
b) $FD//EC$.
c) ${(A D F) / /(B C E)}$.
d) $\dfrac{AN}{NC}=3$.
Câu 70. Cho hình chóp ${S . A B C D}$ có đáy ${A B C D}$ là hình bình hành tâm ${O}$. Gọi ${M, N}$ lần lượt là trung điểm của ${S A}$ và ${S D}$.
a) ${ON}$ chéo nhau với ${SB}$.
b) Gọi ${P}$ và ${Q}$ là trung điểm của ${A B}$ và ${O N}$. Khi đó ${P Q / /(S B C)}$.
c) ${(O M N) / /(S B C)}$.
d) Gọi ${R}$ là trung điểm ${A D}$. Khi đó ${(M O R) / /(S C D)}$.
Câu 71. Với $x\ne \dfrac{\pi }{2}+k\pi ,\,\,k\in \mathbb{Z}$, ta có $\dfrac{2\sin (x-4\pi )+\cos \left( x-\dfrac{5\pi }{2} \right)}{\sin \left( \dfrac{3\pi }{2}-x \right)}=k\tan x$, tìm $k$?
Câu 72. Giá trị biểu thức $\sqrt{{{\sin }^{4}}x+6{{\cos }^{2}}x+3{{\cos }^{4}}x}+\sqrt{{{\cos }^{4}}x+6{{\sin }^{2}}x+3{{\sin }^{4}}x}$ bằng bao nhiêu ?
Câu 73. Phương trình ${\cos \left( 2x-\dfrac{\pi }{2} \right)=\sin \left( \dfrac{\pi }{2}-x \right)}$ có bao nhiêu nghiệm thuộc khoảng $\left( -2\pi \,;\,\dfrac{\pi }{2} \right)$ ?
Câu 74. Tính $\lim \dfrac{1+2+...+n}{{{n}^{2}}+3n}$ ?
Câu 75. Cho $\underset{x\,\,\to \,\,2}{\mathop{\lim }}\,\dfrac{{{x}^{2}}+bx+c}{x\,\,-\,\,2}=1$. Tính giá trị $\dfrac{b}{c}$?
Câu 76. Công ty môi trường đô thị cần trồng cây trên khuôn viên hình tam giác theo hình thức như sau: hàng thứ nhất trồng 1 cây, hàng thứ hai trồng 3 cây, hàng thứ 3 trồng 5 cây, hàng thứ tư trồng 7 cây, … (xem hình vẽ). Công ty dự tính trồng 10 hàng, hỏi công ty cần mua bao nhiêu cây giống ?
Câu 77. Hội trường của một trường học có 14 dãy ghế, dãy đầu tiên có 16 ghế. Mỗi dãy sau có hơn dãy liền trước 5 ghế. Hỏi hội trường có tất cả bao nhiêu ghế ?
Câu 78. Một người vào trường đua ngựa quốc tế đặt cược, anh ta nghĩ ra một chiến lược, đó là lần đầu anh ta đặt cược 2 USD, nếu thua cược anh ta sẽ gấp đôi số tiền cược so với lần trước đó đến khi nào thắng cược thì thôi. Anh ta đã thua 9 lần liên tiếp và thắng cược ở lần thứ 10. Sau đó anh ta rời khỏi trường đua. Biết rằng nếu thắng anh ta sẽ nhận được số tiền bằng đúng số tiền cược bỏ ra. Khi ra về anh ta lãi bao nhiêu USD ?
Câu 79. Một chuyên gia có lương 150 triệu đồng năm đầu tiên. Trong 5 năm đầu, sau mỗi năm lương được tăng thêm 20% so với năm trước. Trong năm thứ ba chuyên gia được nhận lương mấy trăm triệu đồng ?
Câu 80. Tại một cơ sở sản xuất nước tinh khiết, nhân viên phụ trách sản xuất cho biết, nếu mỗi ngày cơ sở này sản xuất $x\,\,\left( {{m}^{3}} \right)$ nước tinh khiết thì phải chi phí các khoản sau: 3 triệu đồng chi phí cố định; 0,12 triệu đồng chi phí bảo dưỡng máy móc cho mỗi mét khối sản phẩm. Gọi $C\left( x \right)$ là chi phí sản suất $x\,\,\left( {{m}^{3}} \right)$ sản phẩm mỗi ngày và $\overline{C}\left( x \right)$là chi phí trung bình mỗi mét khối sản phẩm. Tính $\underset{x\to +\infty }{\mathop{\lim }}\,\overline{C}\left( x \right)$ ?
Câu 81. Tại một nhà máy, người ta đo được rằng 80% lượng nước sau khi sử dụng được xử lí và tái sử dụng. Với ${100 {~m}^3}$ ban đầu được sử dụng lần đầu tại nhà máy, khi quá trình xử lí và tái sử dụng lặp lại mãi mãi, nhà máy sử dụng được tổng lượng nước là bao nhiêu mét khối ?
Câu 82. Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem hình bên). Kí hiệu ${{p}_{n}}$ là chu vi của hình vuông thứ $n$ và ${{Q}_{n}}$ là tổng chu vi của $n$ hình vuông đầu tiên. Tìm lim ${{Q}_{n}}$ (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông) (làm tròn đến hàng đơn vị) ?
Câu 83. Trong hồ có chứa 60000 lít nước ngọt. Người ta bơm nước biển có nồng độ muối là 30 gam/lít vào hồ với tốc độ 15 lít/phút. Nồng độ muối trong hồ như thế nào nếu thời gian bơm cứ diễn ra mãi mãi ? Biết nồng độ muối bằng khối lượng muối chia cho thể tích nước.
Câu 84. Bạn An thả quả bóng cao su từ độ cao $5\,\,m$ so với mặt đất theo phương thẳng đứng. Mỗi lần chạm đất quả bóng lại nảy lên theo phương thẳng đứng có độ cao bằng $\dfrac{4}{5}$ độ cao lần rơi trước đó. Tổng quãng đường quả bóng di chuyển là bao nhiêu mét ?
Câu 85. Cho hình chóp ${S . A B C D}$ có đáy ${A B C D}$ là hình bình hành. Gọi ${I, K}$ lần lượt là trung điểm của ${B C}$ và ${C D}$. Gọi ${M}$ là trung điểm của ${S B}$. Gọi ${F}$ là giao điểm của ${D M}$ và ${(S I K)}$. Tính tỉ số ${\dfrac{M F}{M D}}$?
Câu 86. Cho hình chóp ${S.ABCD}$, có đáy ${ABCD}$ là hình thang, ${AB}$ là đáy lớn. Biết $AB=5a,$ $CD=2a$. Gọi $E$ là điểm thuộc cạnh ${SB}$ thỏa mãn $\dfrac{ES}{EB}=\dfrac{m}{n}$ với $\dfrac{m}{n}$ là phân số tối giản. Biết rằng ${CE}$ song song với mặt phẳng $\left( SAD \right)$. Giá trị của $2m+3n$ bằng bao nhiêu ?
Câu 87. Cho hình chóp ${S.ABCD}$ có đáy ${ABCD}$ là hình bình hành. Gọi $G$ là trọng tâm của tam giác ${ABC}$ và $E$ là điểm thuộc cạnh ${SA}$ thỏa mãn $SE=\dfrac{m}{n}.SA$ với $\dfrac{m}{n}$ là phân số tối giản. Biết rằng ${GE}$ song song với mặt phẳng $\left( SCD \right)$. Tính tỉ số $\dfrac{n}{m}$?
Câu 88. Cho hình chóp ${S.ABC}$. Gọi ${G}$ là trọng tâm tam giác ${ABC}$, mặt phẳng ${\left( \alpha \right)}$ qua ${G}$ và song song với mặt phẳng ${\left( SAB \right)}$, ${\left( \alpha \right)\cap SC=P}$. Tính tỉ số ${\dfrac{SP}{SC}}$ (làm tròn đến hàng phần trăm) ?
Câu 89. Cho hình chóp ${S.ABCD}$. Đáy ${ABCD}$ là hình thang có đáy lớn ${CD}$ bằng hai lần đáy nhỏ ${AB.}$ Gọi ${O=AC\cap BD}$, mặt phẳng ${\left( \alpha \right)}$ qua ${O}$ và song song với mặt phẳng ${\left( SAB \right)}$, ${\left( \alpha \right)\cap SC=P}$. Tính tỉ số ${\dfrac{SP}{PC}}$ ?
Câu 90. Cho hình chóp ${S.ABCD}$ có đáy là hình thang, ${AB//CD}$ và $AB=2CD$. Gọi $O$ là giao điểm của ${AC}$ và ${BD}$. Lấy $E$ thuộc cạnh ${SA}$, $F$ thuộc cạnh ${SC}$ sao cho $\dfrac{SE}{SA}=\dfrac{SF}{SC}=\dfrac{2}{3}$. Gọi $\left( \alpha \right)$ là mặt phẳng qua $O$ và song song với mặt phẳng $\left( BEF \right)$. Gọi $P$ là giao điểm của $SD$ với $\left( \alpha \right)$. Tính tỉ số $\dfrac{SP}{SD}$ (làm tròn đến hàng phần trăm) ?
Phần 1:
| C 1 B | C 2 C | C 3 B | C 4 D | C 5 A | C 6 D | C 7 B | C 8 A | C 9 B | C 10 A | C 11 B |
| C 12 B | C 13 C | C 14 A | C 15 D | C 16 A | C 17 D | C 18 C | C 19 A | C 20 C | C 21 B | C 22 D |
| C 23 D | C 24 B | C 25 D | C 26 B | C 27 A | C 28 B | C 29 A | C 30 A | C 31 B | C 32 D | C 33 D |
| C 34 A | C 35 A | C 36 A | C 37 C | C 38 B | C 39 C | C 40 C | C 41 D | C 42 B | C 43 B | C 44 D |
| C 45 C | C 46 A | C 47 A | C 48 A | C 49 A | C 50 B | C 51 B | C 52 D | C 53 D | C 54 C | C 55 A |
Phần 2:
| Câu 56: S Đ Đ Đ | Câu 57: Đ Đ S S | Câu 58: S Đ S S | Câu 59: Đ S Đ Đ | Câu 60: Đ Đ Đ S |
| Câu 61: Đ Đ S Đ | Câu 62: Đ Đ S S | Câu 63: S S Đ S | Câu 64: S S S Đ | Câu 65: S S Đ S |
| Câu 66: Đ S Đ S | Câu 67: Đ Đ S Đ | Câu 68: S Đ S S | Câu 69: Đ Đ Đ S | Câu 70: Đ S Đ Đ |
Phần 3:
| Câu 71: 3 | Câu 72: 4 | Câu 73: 5 | Câu 74: 0,5 | Câu 75: –1,5 |
| Câu 76: 100 | Câu 77: 679 | Câu 78: 2 | Câu 79: 216 | Câu 80: 0,12 |
| Câu 81: 500 | Câu 82: 14 | Câu 83: 30 | Câu 84: 45 | Câu 85: 1 |
| Câu 86: 13 | Câu 87: 1,5 | Câu 88: 0,33 | Câu 89: 0,5 | Câu 90: 0,86 |
Biên soạn: thầy giáo Nguyễn Quốc Hoàn
Thày cô, Học sinh tải về nếu hỏi mật khẩu thì nhập một trong các mk sau để mở file (NÊN copy và chú ý không dấu cách và không thừa khoảng trắng hay kí tự bất kì): hs.edu.vn https://hs.edu.vn/ https://edu365.edu.vn/ https://edu365.edu.vn edu365.edu.vn edu365free freeedu365 edu365.edu.vnfree edu365 hoc moi luc moi noi
(Nếu file quá nhiều lượt tải về trong ngày, xin bấm vào đây xem hướng dẫn để tải ngay)
Chúng tôi luôn mong nhận được sự đồng hành, góp ý và chia sẻ của thầy cô giáo và học sinh.
Xin gửi về địa chỉ:
Mobi, Zalo: 0913 661 886
Tel: 025 99 999 888 , 024 666 07 999 , 028 99 99 99 77
Giờ làm việc: 08h11 - 18h36 hàng ngày; trừ các ngày lễ và ngày thứ bẩy, chủ nhật.
Đánh giá và nhận xét
Đánh giá trung bình
(22 đánh giá)
4.95