Fri, ngày 27/12/2024, 03:12 (GMT +7)
Đề 6 ÔN TẬP CUỐI KÌ 1 TOÁN LỚP 12 NĂM HỌC 2024 – 2025
Câu 1. Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ sau
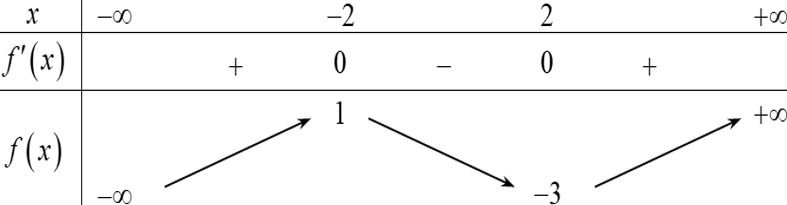 Hàm số đã cho nghịch biến trên khoảng
Hàm số đã cho nghịch biến trên khoảng
A. $\left( -3;1 \right).$ B. $\left( -2;2 \right).$ C. $\left( 2;+\infty \right).$ D. $\left( -\infty ;-2 \right).$
Câu 2. Cho hàm số $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị là đường cong như hình vẽ
A. $y\,=\,0$. B. $x\,=\,2$. C. $x\,=\,0$. D. $y\,=\,-2$.
Câu 3. Cho hàm số $y=f\left( x \right)$ xác định và liên tục trên đoạn $\left[ -2\,;\,2 \right]$ và có đồ thị là đường cong trong hình vẽ sau
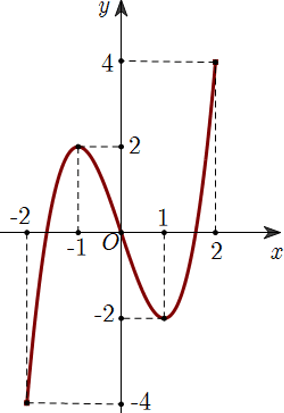 Điểm cực tiểu của đồ thị hàm số $y=f\left( x \right)$ là
Điểm cực tiểu của đồ thị hàm số $y=f\left( x \right)$ là
A. ${x=1}$. B. ${x=-2}$. C. ${M\left( 1\,;\,-2 \right)}$. D. ${M\left( -2\,;\,-4 \right)}$.
Câu 4. Trên khoảng ${(0;\text{ }+\infty )}$, hàm số $y=-\dfrac{1}{3}{{x}^{3}}+x+1$ có
A. giá trị nhỏ nhất là $-1$. B. giá trị lớn nhất là $\dfrac{5}{3}$. C. giá trị nhỏ nhất là $\dfrac{5}{3}$. D. giá trị lớn nhất là 1.
Câu 5. Cho hàm số ${y=f\left( x \right)}$ xác định trên $\mathbb{R}\backslash \left\{ 1 \right\}$ và có đồ thị như hình dưới đây
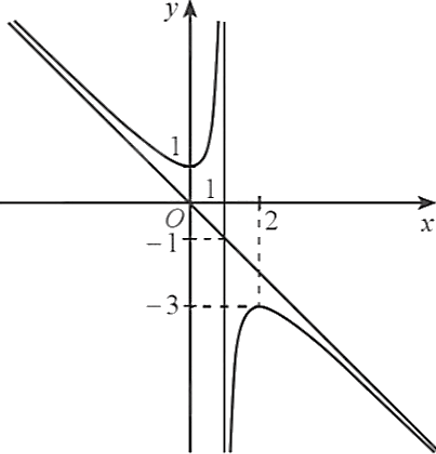 Phương trình đường tiệm cận đứng và phương trình đường tiệm cận xiên của đồ thị đã cho là
Phương trình đường tiệm cận đứng và phương trình đường tiệm cận xiên của đồ thị đã cho là
A. $x=1;\,\,y=-x$. B. $x=-1;\,\,y=x$. C. $x=1;\,\,y=x$. D. $x=1;\,\,y=-2x$.
Câu 6. Cho hàm số $y=\dfrac{ax-1}{bx+c}$ với $a,b,c\in \mathbb{R}$ có bảng biến thiên như hình vẽ
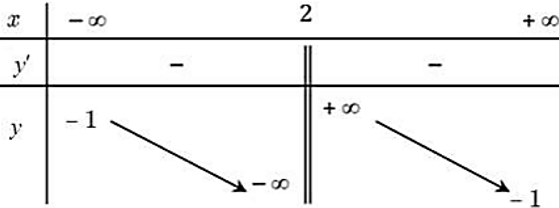 Hỏi trong ba số $a,b,c$ có bao nhiêu số dương ?
Hỏi trong ba số $a,b,c$ có bao nhiêu số dương ?
A. 0. B. 1. C. 2. D. 3.
Câu 7. Kết quả đo chiều cao của 100 cây keo 2 năm tuổi tại một nông trường được cho ở bảng sau
| Chiều cao (m) | [5,4 ; 5,6) | [5,6 ; 5,8) | [5,8 ; 6,0) | [6,0 ; 6,2) | [6,2 ; 6,4) |
| Số cây | 5 | 12 | 25 | 44 | 14 |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
A. 0,2. B. 0,4. C. 1. D. 1,2.
Câu 8. Gọi $G$ là trọng tâm của tứ diện $ABCD$. Trong các khẳng định sau, khẳng định sai là
A. $\overrightarrow{AG}=\dfrac{1}{4}\left( \overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD} \right)$. B. $\overrightarrow{AG}=\dfrac{2}{3}\left( \overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD} \right)$. C. $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$. D. $\overrightarrow{OG}=\dfrac{1}{4}\left( \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD} \right)$.
Câu 9. Cho lăng trụ đứng $ABC.{A}'{B}'{C}'$. Đáy là tam giác ${ABC}$ vuông tại $B$. Khi đó góc giữa vectơ $\overrightarrow{BA}$ và vectơ $\overrightarrow{{B}'{C}'}$ bằng
A. $120{}^0$. B. $90{}^0$. C. $45{}^0$. D. $30{}^0$.
Câu 10. Trong không gian ${Oxyz}$, cho $\overrightarrow{a}=\left( 3;2;1 \right)$, $\overrightarrow{b}=\left( -2;0;1 \right)$. Độ dài của $\overrightarrow{a}+\overrightarrow{b}$ là
A. 1. B. $\sqrt{2}$. C. 2. D. 3.
Câu 11. Trong không gian ${Oxyz}$, cho điểm ${I\left( -5;0;5 \right)}$ là trung điểm của đoạn ${MN}$, biết ${M\left( 1;-4;7 \right)}$. Khi đó tọa độ của điểm ${N}$ là
A. ${N\left( -10;4;3 \right)}$. B. ${N\left( -11;-4;3 \right)}$. C. ${N\left( -2;-2;6 \right)}$. D. ${N\left( -11;4;3 \right)}$.
Câu 12. Trong không gian $Oxyz$, cho điểm $A\left( 1;0;-2 \right)$, $B\left( 1;-1;0 \right)$. Điểm $C$ nằm trên trục $Oz$ sao cho $AB\bot BC$, toạ độ ${C}$ là
A. $\left( 0;0;1 \right)$. B. $\left( 0;0;-1 \right)$. C. $\left( 0;0;\dfrac{1}{2} \right)$. D. $\left( 0;0;-\dfrac{1}{2} \right)$.
Câu 1. Cho hàm số $y={{x}^{3}}-3x+1$
a) Hàm số đồng biến trên $\left( 1;+\infty \right)$.
b) Hàm số có giá trị cực tiểu bằng 3.
c) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 1.
d) Giá trị lớn nhất của hàm số trên $\left[ -2;1 \right]$ bằng 3.
Câu 2. Cho hàm số $f\left( x \right)=x-\sin 2x$.
a) $f(0)=0;\,\ f(\pi )=\pi$.
b) Đạo hàm của hàm số đã cho là $f'\left( x \right)=1+2\cos 2x$.
c) Nghiệm của phương trình $f'\left( x \right)=0$ trên đoạn $\left[ 0;\pi \right]$ là $\dfrac{\pi }{6}$ và $\dfrac{5\pi }{6}$.
d) Giá trị nhỏ nhất của hàm số đã cho trên đoạn $\left[ 0;\pi \right]$ là $\dfrac{\pi }{6}-\dfrac{\sqrt{3}}{2}$.
Câu 3. Giá đóng cửa của một cổ phiếu là giá của cổ phiếu đó cuối một phiên giao dịch. Bảng sau thống kê giá đóng cửa (đơn vị: nghìn đồng) của hai mã cổ phiếu ${A}$ và ${B}$ trong 50 ngày giao dịch liên tiếp.
| Giá đóng cửa | [120 ; 122) | [122 ; 124) | [124 ; 126) | [126 ; 128) | [128 ; 130) |
| Cổ phiếu A | 8 | 9 | 12 | 10 | 11 |
| Cổ phiếu B | 16 | 4 | 3 | 6 | 21 |
a) Số ngày cổ phiếu B có giá dưới 126 nghìn đồng nhiều hơn số ngày số ngày cổ phiếu A có giá dưới 126 nghìn đồng.
b) Xét mẫu số liệu của cổ phiếu ${B}$, ta có số trung bình của mẫu số liệu ghép nhóm là 115,28.
c) Xét mẫu số liệu của cổ phiếu ${A}$, ta có phương sai của mẫu số liệu ghép nhóm là 7,5216.
d) Người ta có thể dùng phương sai và độ lệch chuẩn để so sánh mức độ rủi ro của các loại cổ phiếu có giá trị trung bình gần bằng nhau. Cổ phiếu nào có phương sai, độ lệch chuẩn cao hơn thì được coi là có độ rủi ro lớn hơn. Theo quan điểm trên, thì cổ phiếu ${A}$ có độ rủi ro thấp hơn cổ phiếu ${B}$.
Câu 4. Bên hông của ngôi nhà là một bức tường phẳng, người ta muốn lắp một bóng đèn và một công tắc để bật tắt đèn. Công tắc gắn vào bức tường, đèn cách mặt đất 3 mét và nằm trên một cột coi là đường thẳng song song với mặt phẳng chứa bức tường, cách bức tường 2 mét. Công tơ ngoài đường cách mặt đất 1 mét và đặt trên một cột coi là đường thẳng song song với mặt phẳng chứa bức tường, cách bức tường 8 mét. Coi mặt đất là mặt phẳng, cột đèn và cột công tơ cách nhau 10 mét. Dây điện từ công tơ kéo vào công tắc và từ công tắc kéo ra đèn như hình vẽ.
Chọn hệ trục tọa độ ${Oxyz}$ như sau: mặt phẳng ${Oxy}$ là mặt đất, trục ${Ox}$ là đường giao bức tường và mặt đất, trục ${Oy}$ qua chân cột đèn, trục ${Oz}$ là đường thẳng nằm trên bức tường, đơn vị trên các trục là mét và chiều các trục như hình vẽ. Coi chân cột đèn là điểm ${M}$, chân cột công tơ là điểm ${N}$, hoành độ và tung độ điểm ${N}$ là số dương.
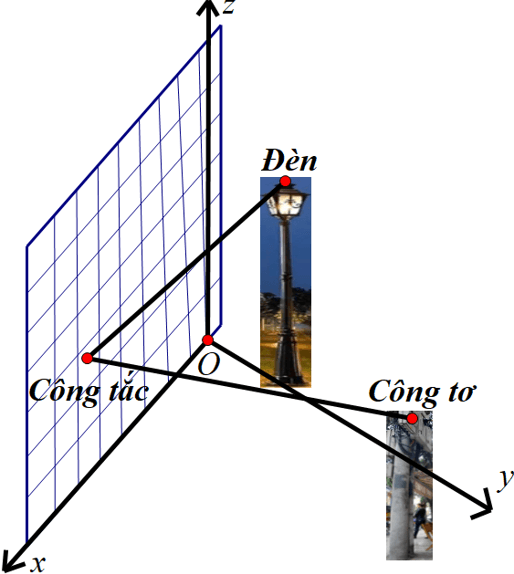 a) Khoảng cách ${MN}$ bằng 10 mét.
a) Khoảng cách ${MN}$ bằng 10 mét.
b) Coi đèn là điểm ${A}$, tọa độ điểm ${A}$ là (0 ; 3 ; 2).
c) Tọa độ điểm ${N}$ là (8 ; 8 ; 0).
d) Người ta đã chọn vị trí đặt công tắc sao cho tổng chiều dài dây điện mắc như hình vẽ là nhỏ nhất, khi đó dây điện dài không quá 12 mét (sai số không quá 0,1 mét).
Câu 1. Đồ thị của hàm số $y=\dfrac{{{x}^{2}}-x}{2x+2}$ có tiệm cận xiên là đường thẳng $y=ax+b$. Tính giá trị $b-2a$ ?
Câu 2. Đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}-9x+5$ có điểm cực đại và điểm cực tiểu lần lượt là $A$ và $B$. Gọi $I$ là giao điểm của $AB$ với trục $Ox$. Tính tỷ số $\dfrac{IA}{IB}$ (kết quả làm tròn đến hàng phần trăm) ?
Câu 3. Cho hàm số $y=\dfrac{{{x}^{2}}-4x+1}{x+2}.$ Gọi $\Delta$ là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số. Tính khoảng cách từ gốc tọa độ $O$ đến $\Delta$ (kết quả làm tròn đến hàng phần trăm) ?
Câu 4. Một doanh nghiệp cần sản xuất một mặt hàng trong đúng 10 ngày và phải sử dụng hai máy $A$ và $B$. Máy $A$ làm việc trong $x$ ngày cho số tiền lãi là ${{x}^{2}}+10x$ (triệu đồng), máy $B$ làm việc trong $y$ ngày cho số tiền lãi là $-26{{y}^{2}}+330y$ (triệu đồng). Hỏi doanh nghiệp đó cần sử dụng máy $A$ làm việc trong bao nhiêu ngày để số tiền lãi thu được nhiều nhất ? Biết rằng hai máy $A$ và $B$ không đồng thời làm việc.
Câu 5. Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá, camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự định trồng bốn chiếc cột cao 30 m và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ camera ở vị trí mong muốn. Mô hình thiết kế được xây dựng như sau: Trong hệ trục toạ độ ${Oxyz}$, các đỉnh của bốn chiếc cột lần lượt là các điểm $M(90;0;30)$, $N(90;120;30)$, $P(0;120;30)$, $Q(0;0;30)$ (tham khảo hình dưới). Giả sử ${K}$ là vị trí ban đầu của camera có cao độ bằng 25 và ${KM=KN=KP=KQ}$. Để theo dõi quả bóng đến vị trí $A$, camera được hạ thấp theo phương thẳng đứng xuống điểm ${G}$ có cao độ bằng 19.
(Nguồn: https:⁄/www.abiturloesumg.de; Abitur Bayern 2016 Geometrie VI).
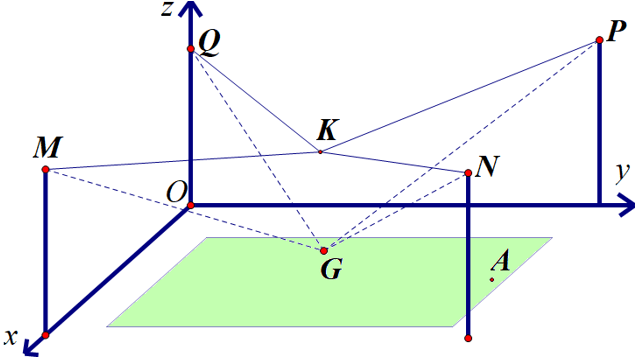 Biết rằng vectơ $\overrightarrow{KG}$ có tọa độ là $(a;b;c);\,\,a,b,c\in \mathbb{R}$. Tính $a+b+c$ ?
Biết rằng vectơ $\overrightarrow{KG}$ có tọa độ là $(a;b;c);\,\,a,b,c\in \mathbb{R}$. Tính $a+b+c$ ?
Câu 6. Để theo dõi hành trình của một chiếc máy bay, người ta lập hệ tọa độ ${Oxyz}$ có gốc ${O}$ trùng với vị trí của trung tâm kiểm soát không lưu, mặt phẳng ${ (Oxy)}$ trùng với mặt đất (mặt đất được coi là mặt phẳng), trục ${Ox}$ hướng về phía tây, trục ${Oy}$ hướng về phía bắc và trục ${Oz}$ hướng thẳng lên trên trời, đơn vị đo trong không gian ${Oxyz}$ là kilômét. Sau khi cất cánh và đạt độ cao 11000 mét, chiếc máy bay duy trì hướng bay về phía bắc và giữ độ cao này với tốc độ không đổi là 900 km/h trong 30 phút. Tọa độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nửa giờ đó là $\overrightarrow{u}\,\,=\,\,\left( a\,;\,b\,;\,c \right)$, tính $\dfrac{b}{c}$ (làm tròn kết quả đến hàng phần chục) ?
_ _ _ _ _ _ Hết _ _ _ _ _ _
Thày cô, Học sinh tải về nếu hỏi mật khẩu thì nhập một trong các mk sau để mở file (NÊN copy và chú ý không dấu cách và không thừa khoảng trắng hay kí tự bất kì): hs.edu.vn https://hs.edu.vn/ https://edu365.edu.vn/ https://edu365.edu.vn edu365.edu.vn edu365free freeedu365 edu365.edu.vnfree edu365 hoc moi luc moi noi
(Nếu file quá nhiều lượt tải về trong ngày, xin bấm vào đây xem hướng dẫn để tải ngay)
Chúng tôi luôn mong nhận được sự đồng hành, góp ý và chia sẻ của thầy cô giáo và học sinh.
Xin gửi về địa chỉ:
Nhà giáo: Nguyễn Quốc Hoàn
Mobi, Zalo: 0913 661 886
Tel: 025 99 999 888 , 024 666 07 999 , 028 99 99 99 77
Giờ làm việc: 08h11 - 18h36 hàng ngày; trừ các ngày lễ và ngày thứ bẩy, chủ nhật.
ĐÁP ÁN CHẤM ĐỀ 6 CUỐI KÌ 1 TOÁN 12 NĂM HỌC 2024 – 2025
Phần 1
| 1B | 2B | 3C | 4B | 5A | 6C | 7C | 8B | 9B | 10D | 11D | 12C |
Phần 2
| Câu 1: Đ S Đ Đ | Câu 2: Đ S Đ Đ | Câu 3: S S Đ Đ | Câu 4: Đ S Đ S |
Phần 3
| Câu 1: | Câu 2: | Câu 3: | Câu 4: | Câu 5: | Câu 6: |
Đánh giá và nhận xét
Đánh giá trung bình
(0 đánh giá)
0