Thứ ba, ngày 24/12/2024, 03:12 (GMT +7)
ÔN TẬP CUỐI KÌ 1 TOÁN LỚP 12 NĂM HỌC 2024 – 2025 Đề 4
Câu 1. Hàm số $y=2{{x}^{3}}-9{{x}^{2}}-24x+1$ nghịch biến trên khoảng
A. $\left( -\infty ;-1 \right)$. B. $\left( -1;\,4 \right)$. C. $\left( -\infty ;4 \right)$. D. $\left( 4;\,+\infty \right)$.
Câu 2. Hàm số nào dưới đây nghịch biến trên $\mathbb{R}$?
A. $y=\dfrac{x+1}{2-x}$. B. $y=-{{x}^{3}}-3x+2024$. C. $y=-{{x}^{3}}-2{{x}^{2}}+x+2024$. D. $y=2{{x}^{2}}-3x+2024$.
Câu 3. Cho hàm số ${y=f\left( x \right)}$ có bảng biến thiên như sau
 Giá trị cực tiểu của hàm số đã cho bằng
Giá trị cực tiểu của hàm số đã cho bằng
A. ${-1}$. B. 1. C. 3. D. ${-2}$.
Câu 4. Giá trị nhỏ nhất của hàm số $\displaystyle y=- x^{3} + \dfrac{3 x^{2}}{2} + 6 x + 1$ trên đoạn ${[-2;4]}$ bằng
A. $-15$. B. $-\dfrac{113}{2}$. C. $\dfrac{47}{2}$. D. 11.
Câu 5. Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau
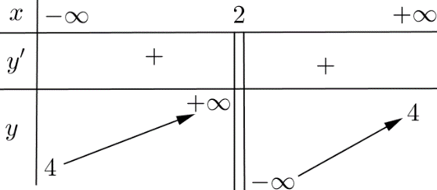 Số đường tiệm cận của đồ thị của hàm số đã cho là
Số đường tiệm cận của đồ thị của hàm số đã cho là
A. 0. B. 1. C. 2. D. 3.
Câu 6. Tiệm cận xiên của đồ thị hàm số ${y=\dfrac{3x-{{x}^{2}}}{2x-1}}$ là đường thẳng ${y=ax+b}$. Giá trị của biểu thức ${{a}^{2}}-b$ bằng
A. 1. B. $-1$. C. 2. D. $-2.$
Câu 7. Hàm số nào dưới đây có đồ thị như hình dưới ?
 A. $y=\dfrac{x+2}{x-1}.$ B. $y=\dfrac{x-2}{x+1}.$ C. $y=\dfrac{x-2}{x-1}.$ D. $y=\dfrac{x+2}{x-2}.$
A. $y=\dfrac{x+2}{x-1}.$ B. $y=\dfrac{x-2}{x+1}.$ C. $y=\dfrac{x-2}{x-1}.$ D. $y=\dfrac{x+2}{x-2}.$
Câu 8. Cho tứ diện đều $ABCD$ cạnh $a$. Khi đó $\left| \overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD} \right|$ bằng
A. $a\sqrt{6}.$ B. $a\sqrt{3}.$ C. $\dfrac{a\sqrt{6}}{2}.$ D. $\dfrac{a\sqrt{3}}{2}.$
Câu 9. Cho hình lăng trụ $ABC.{A}'{B}'{C}'$, $M$ là trung điểm của $B{B}'$. Đặt $\overrightarrow{CA}=\overrightarrow{a}$, $\overrightarrow{CB}=\overrightarrow{b}$, $\overrightarrow{A{A}'}=\overrightarrow{c}$. Khi đó
A. $\overrightarrow{AM}=\overrightarrow{b}+\overrightarrow{c}-\dfrac{1}{2}\overrightarrow{a}$. B. $\overrightarrow{AM}=\overrightarrow{a}-\overrightarrow{c}+\dfrac{1}{2}\overrightarrow{b}$. C. $\overrightarrow{AM}=\overrightarrow{a}+\overrightarrow{c}-\dfrac{1}{2}\overrightarrow{b}$. D. $\overrightarrow{AM}=\overrightarrow{b}-\overrightarrow{a}+\dfrac{1}{2}\overrightarrow{c}$.
Câu 10. Cho hình lập phương ${ABCD.A'B'C'D'}$ có tâm ${O}$. Khi đó
A. ${\overrightarrow{AO}=\dfrac{1}{3}\left( \overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'} \right)}$. B. ${\overrightarrow{AO}=\dfrac{1}{2}\left( \overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'} \right)}$. C. ${\overrightarrow{AO}=\dfrac{1}{4}\left( \overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'} \right)}$. D. ${\overrightarrow{AO}=\dfrac{2}{3}\left( \overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'} \right)}$.
Câu 11. Trong không gian ${Oxyz}$, cho tam giác $ABC$ vuông tại ${C}$ với điểm $A\left( 1;2;0 \right),B\left( 2;-1;1 \right)$ và điểm $C$ trên trục $Ox$ có hoành độ dương. Diện tích tam giác $ABC$ bằng
A. $\sqrt{6}$. B. $2\sqrt{6}$. C. $\sqrt{30}$. D. $\dfrac{\sqrt{30}}{2}$.
Câu 12. Trong không gian ${Oxyz}$, cho hình hộp ${ABCD.A'B'C'D'}$ biết $A(1;0;1)$, $B(2;1;2)$, $D(1;-1;1)$, $C'(4;5;-5)$. Tọa độ đỉnh $A'$ là
A. $A'(-2;1;1)$. B. $A'(3;5;-6)$. C. $A'(5;-1;0)$. D. $A'(2;0;2)$.
Câu 1. Cho hàm số $y={{x}^{3}}-3x+1$.
a) Điểm cực tiểu của hàm số là $x=1$.
b) Hàm số đồng biến trên khoảng $\left( -1;1 \right)$.
c) Giả sử hàm số đã cho có hai điểm cực trị là ${{x}_{1}};{{x}_{2}}$. Khi đó giá trị ${{x}_{1}}. {{x}_{2}}=-1$.
d) Gọi $A,\,\,B$ lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số. Khi đó, diện tích tam giác $ABC$ bằng 12 với $C(-1;2)$.
Câu 2. Bảng dưới đây cho ta bảng tần số ghép nhóm số liệu thống kê cân nặng của các học sinh lớp 12A trong một trường phổ thông (đơn vị: kilôgam).
| Nhóm | [30 ; 40) | [40 ; 50) | [50 ; 60) | [60 ; 70) | [70 ; 80) | [80 ; 90) |
| Số học sinh | 2 | 10 | 16 | 8 | 2 | 2 |
a) Số học sinh lớp 12A là 40.
b) Nhóm chứa Mốt của mẫu số liệu là [50 ; 60).
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là $\dfrac{39}{2}.$
d) Phương sai của mẫu số liệu ghép nhóm là 126.
Câu 3. Trong không gian ${Oxyz}$, cho $A\left( 1;-1;2 \right)$, $B\left( -2;0;3 \right)$, $C\left( 0;1;-2 \right)$.
a) Tọa độ trọng tâm tam giác $ABC$ là $G\left( \dfrac{-1}{3};0;1 \right)$.
b) Độ dài đoạn thẳng $AB=\sqrt{11}$.
c) Tích có hướng của hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ bằng $\left( -6;13;-5 \right)$.
d) $M\left( a;b;c \right)$ là điểm thuộc mặt phẳng ${\left( Oxy \right)}$ sao cho biểu thức ${S=2.\overrightarrow{MA}.\overrightarrow{MB}+\overrightarrow{MB}.\overrightarrow{MC}+\overrightarrow{MC}.\overrightarrow{MA}}$ đạt giá trị nhỏ nhất, ta có $a-b+c=\dfrac{1}{4}$.
Câu 4. Một chiếc máy bay đang bay trên không trung. Xét hệ trục tọa độ ${Oxyz}$ được gắn như hình vẽ, trong đó gốc $O$ là vị trí của trạm kiểm soát không lưu và $M\left( x;y;z \right)$ (km) biểu thị vị trí máy bay trên không trung. Tại thời điểm 8h máy bay đang ở vị trí $\left( 50;120;4 \right)$ và chuyển động với vận tốc $\overrightarrow{v}=\left( 300;400;3 \right)$ (km/h).
 a) Tại thời điểm 8h, khoảng cách giữa máy bay và trạm kiểm soát không lưu nói trên xấp xỉ 130 km (sai số không quá 1 km).
a) Tại thời điểm 8h, khoảng cách giữa máy bay và trạm kiểm soát không lưu nói trên xấp xỉ 130 km (sai số không quá 1 km).
b) Tại thời điểm 9h độ cao của máy bay so với mặt đất là 8 km.
c) Tại thời điểm 10h, khoảng cách giữa máy bay và một tháp truyền hình $F$ có tọa độ $\left( 1250;1020;0 \right)$ xấp xỉ 700 km (sai số không quá 10 km).
d) Khi đạt độ cao 10 km, máy bay đổi vận tốc mới là $\overrightarrow{{{v}_{2}}}=\left( 400;300;-5 \right)$ để hướng đến sân bay $B$. Tọa độ của máy bay khi vừa đáp xuống sân bay $B$ là $\left( 1450;1520;0 \right)$.
Câu 1. Đồ thị của hàm số $y=\dfrac{x-1}{{{x}^{2}}+x-2}$ có bao nhiêu đường tiệm cận đứng ?
Câu 2. Người ta đã thống kê đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở một lâm trường cho bởi bảng sau:
| Đường kính (cm) | [40 ; 45) | [45 ; 50) | [50 ; 55) | [55 ; 60) | [60 ; 65) |
| Tần số | 5 | 20 | 18 | 7 | 3 |
Có bao nhiêu cây có đường kính nhỏ hơn 50 cm ?
Câu 3. Trong không gian $Oxyz$, cho tam giác $ABC$ có ${A\left( -2;0;-3 \right)}$, ${B\left( -4;1;-1 \right) }$, ${C\left( -4;-4;1 \right) }$. Tính độ dài đường phân giác trong góc $A$ của tam giác ${ABC}$ ? (làm tròn đến hàng phần chục).
Câu 4. Khi máu di chuyển từ tim qua các động mạch chính rồi đến các mao mạch và quay trở lại qua các tĩnh mạch, huyết áp tâm thu (tức là áp lực của máu lên động mạch khi tim co bóp) liên tục giảm xuống. Giả sử một người có huyết áp tâm thu $P$ (tính bằng mmHg) được cho bởi hàm số $P\left( t \right)=\dfrac{25{{t}^{2}}+125}{{{t}^{2}}+1},$ $0\le t\le 10$, trong đó thời gian $t$ được tính bằng giây. Tính tốc độ thay đổi của huyết áp sau 5 giây kể từ khi máu rời tim ?
Câu 5. Giám đốc một nhà hát A đang phân vân trong việc xác định mức giá vé xem các chương trình được trình chiếu trong nhà hát. Việc này rất quan trọng nó sẽ quyết định nhà hát thu được bao nhiêu lợi nhuận từ các buổi trình chiếu. Theo những cuốn sổ ghi chép của mình, ông ta xác định được rằng: nếu giá vé vào cửa là 20 USD cho mỗi người thì trung bình có 1000 người đến xem. Nhưng nếu tăng thêm 1 USD cho mỗi người thì sẽ mất 100 khách hàng hoặc giảm đi 1 USD cho mỗi người thì sẽ có thêm 100 khách hàng trong số trung bình. Biết rằng, trung bình mỗi khách hàng đến còn đem lại 2 USD lợi nhuận cho nhà hát trong các dịch vụ đi kèm. Hỏi giá vé vào cửa là bao nhiêu USD để thu nhập đạt nhiều nhất ?
Câu 6. Trong một bài thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng vận tốc chạy đường bộ của chiến sĩ gấp bốn lần vận tốc bơi của chiến sĩ. Coi dòng sông là thẳng có lòng rộng 100m, hai bên bờ sông cách nhau 100 mét và mục tiêu cách chiến sỹ 1 kilômét theo đường chim bay. Hãy cho biết chiến sỹ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất (làm tròn kết quả đến hàng đơn vị) ?
Thày cô, Học sinh tải về nếu hỏi mật khẩu thì nhập một trong các mk sau để mở file (NÊN copy và chú ý không dấu cách và không thừa khoảng trắng hay kí tự bất kì): hs.edu.vn https://hs.edu.vn/ https://edu365.edu.vn/ https://edu365.edu.vn edu365.edu.vn edu365free freeedu365 edu365.edu.vnfree edu365 hoc moi luc moi noi
(Nếu file quá nhiều lượt tải về trong ngày, xin bấm vào đây xem hướng dẫn để tải ngay)
Chúng tôi luôn mong nhận được sự đồng hành, góp ý và chia sẻ của thầy cô giáo và học sinh.
Xin gửi về địa chỉ:
Nhà giáo: Nguyễn Quốc Hoàn
Mobi, Zalo: 0913 661 886
Tel: 025 99 999 888 , 024 666 07 999 , 028 99 99 99 77
Giờ làm việc: 08h11 - 18h36 hàng ngày; trừ các ngày lễ và ngày thứ bẩy, chủ nhật.
Đánh giá và nhận xét
Đánh giá trung bình
(2 đánh giá)
5