Thứ tư, ngày 25/12/2024, 10:12 (GMT +7)
Đề 5 ÔN TẬP CUỐI KÌ 1 TOÁN LỚP 12 NĂM HỌC 2024 – 2025
Câu 1. Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đạo hàm ${f}'\left( x \right)=\left( x+1 \right){{\left( x-4 \right)}^{2}}{{\left( x-8 \right)}^{3}},\,\forall x\in \mathbb{R}$. Ta có
A. $f\left( 6 \right)<f\left( 8 \right)$. B. $f\left( 8 \right)>f\left( 12 \right)$. C. $f\left( -1 \right)<f\left( 4 \right)$. D. $f\left( -1 \right)>f\left( 8 \right)$.
Câu 2. Cho hàm số ${y=\dfrac{{{x}^{3}}}{3}-2{{x}^{2}}+3x+\dfrac{2}{3}}$. Toạ độ điểm cực đại của đồ thị hàm số là
A. ${\left( -1;2 \right).}$ B. $\left( 3;\dfrac{2}{3} \right).$ C. ${\left( 1;-2 \right).}$ D. ${\left( 1;2 \right).}$
Câu 3. Cho hàm số $f\left( x \right)$ liên tục trên $\left[ -1;5 \right]$ và có đồ thị trên đoạn $\left[ -1;5 \right]$ như hình vẽ bên dưới.
 Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right)$ trên đoạn $\left[ -1;5 \right]$ bằng
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right)$ trên đoạn $\left[ -1;5 \right]$ bằng
A. $-1$. B. 1. C. 2. D. 4.
Câu 4. Tiệm cận đứng của đồ thị hàm số ${y=\dfrac{4x+3}{x-2}}$ là
A. ${x=4}$. B. ${x=2}$. C. ${y=4}$. D. ${y=2}$.
Câu 5. Tiệm cận ngang của đồ thị hàm số ${y=\dfrac{4x+3}{x-2}}$ là
A. ${x=4}$. B. ${x=2}$. C. ${y=4}$. D. ${y=2}$.
Câu 6. Số tiệm cận của đồ thị hàm số $y=\dfrac{2{{x}^{2}}-5x+2}{{{x}^{2}}-4}$ là
A. 0. B. 1. C. 2. D. 3.
Câu 7. Hình dưới đây là đồ thị của hàm số
 A. $y\,\,=\,\,-{{x}^{3}}+3x-1$. B. $y\,\,=\,\,-{{x}^{3}}-3{{x}^{2}}-1$. C. $y\,\,=\,\,-{{x}^{3}}+3{{x}^{2}}-1$. D. $y\,\,=\,\,{{x}^{3}}-3x-1$.
A. $y\,\,=\,\,-{{x}^{3}}+3x-1$. B. $y\,\,=\,\,-{{x}^{3}}-3{{x}^{2}}-1$. C. $y\,\,=\,\,-{{x}^{3}}+3{{x}^{2}}-1$. D. $y\,\,=\,\,{{x}^{3}}-3x-1$.
Câu 8. Hình dưới đây là đồ thị của hàm số
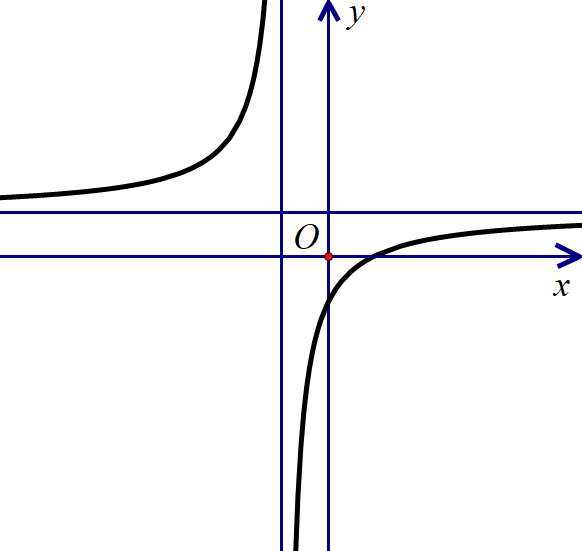 A. $y=\dfrac{x+1}{x-1}$. B. $y=\dfrac{x-1}{x+1}$. C. $y=\dfrac{x+2}{x+1}$. D. $y=\dfrac{{{x}^{2}}-2x}{x+1}$.
A. $y=\dfrac{x+1}{x-1}$. B. $y=\dfrac{x-1}{x+1}$. C. $y=\dfrac{x+2}{x+1}$. D. $y=\dfrac{{{x}^{2}}-2x}{x+1}$.
Câu 9. Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được cho ở biểu đồ sau
 Số sinh viên làm thêm từ 8 giờ trở lên trong một tuần là
Số sinh viên làm thêm từ 8 giờ trở lên trong một tuần là
A. 68. B. 31. C. 21. D. 10.
Câu 10. Cho tứ diện đều ${ABCD}$ có cạnh bằng ${a}$. Khi đó ${\overrightarrow{AB}\left( \overrightarrow{AB}-\overrightarrow{DA} \right)}$ bằng
A. ${\dfrac{{{a}^{2}}}{2}}$. B. ${\dfrac{{{a}^{2}}\sqrt{2}}{4}}$. C. ${\dfrac{{{a}^{2}}\sqrt{3}}{4}}$. D. ${\dfrac{3{{a}^{2}}}{2}}$.
Câu 11. Trong không gian ${Oxyz}$, cho hai vectơ $\overrightarrow{a}\left( 1\,;\,3\,;\,1 \right)$ và $\overrightarrow{b}\left( 3\,;\,5\,;\,1 \right)$. Tọa độ của một vectơ vuông góc với cả hai vectơ $\overrightarrow{a}\left( 1\,;\,3\,;\,1 \right)$ và $\overrightarrow{b}\left( 3\,;\,5\,;\,1 \right)$ là
A. $\left( 1\,;\,-1\,;\,2 \right)$. B. $\left( 1\,;\,1\,;\,4 \right)$. C. $\left( 1\,;\,-1\,;\,-2 \right)$. D. $\left( 2\,;\,-2\,;\,2 \right)$.
Câu 12. Trong không gian ${Oxyz}$, cho hình hộp ${ABCD.A'B'C'D'}$ có $A(1;0;1),$ $B(2;1;2),$ $D(1;-1;1),$ $C'(4;5;-5)$. Toạ độ tâm ${I}$ của hình hộp là
A. $\left( -\dfrac{3}{2};\dfrac{5}{2};-3 \right)$. B. $\left( \dfrac{3}{2};\dfrac{5}{2};-3 \right)$. C. $\left( -\dfrac{5}{2};\dfrac{5}{2};-2 \right)$. D. $\left( \dfrac{5}{2};\dfrac{5}{2};-2 \right)$.
Câu 1. Cho hàm số $y=f\left( x \right)$ xác định và liên tục trên $\mathbb{R}$, biết đồ thị hàm số $y={f}'\left( x \right)$ là đường cong như hình bên dưới.
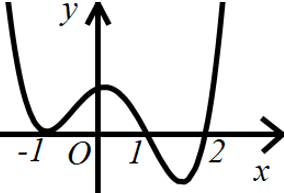 a) Hàm số $y=f\left( x \right)$ nghịch biến trên khoảng $\left( 1;2 \right).$
a) Hàm số $y=f\left( x \right)$ nghịch biến trên khoảng $\left( 1;2 \right).$
b) Hàm số $y=f\left( x \right)$ có ba điểm cực trị.
c) Hàm số $y=f\left( x \right)$ đạt cực đại tại điểm $x=1.$
d) Giá trị lớn nhất của hàm số $y=f\left( x \right)$ trên đoạn $\left[ 1;2 \right]$ bằng $f\left( 2 \right).$
Câu 2. Khảo sát tuổi thọ của một loại bóng đèn được hai phân xưởng A và B cùng sản xuất cho ở bảng sau.
| Tuổi thọ (tháng) | [24 ; 27) | [27 ; 30) | [30 ; 33) | [33 ; 36) | [36 ; 39) |
| Số bóng đèn của phân xưởng A | 4 | 8 | 10 | 6 | 2 |
| Số bóng đèn của phân xưởng B | 5 | 7 | 9 | 7 | 2 |
a) Khoảng biến thiên của tuổi thọ bóng đèn phân xưởng A là 15.
b) Khoảng tứ phân vị của tuổi thọ bóng đèn phân xưởng A và phân xưởng B lần lượt là ${\dfrac{39}{7}}$ và ${4{,}9375}$.
c) Tuổi thọ trung bình của bóng đèn mà hai phân xưởng sản xuất là bằng nhau.
d) Nếu so sánh độ lệch chuẩn tuổi thọ bóng đèn mẫu số liệu của phân xưởng B đồng đều hơn mẫu số liệu của phân xưởng A.
Câu 3. Trong không gian $Oxyz$; cho tam giác $ABC$ có $A\left( 1;\,0;\,3 \right)$, $B\left( 0;\,2;\,0 \right)$, $C\left( 0;\,0;-3 \right)$.
a) Toạ độ vectơ $\overrightarrow{OA}=\left( 1;0;3 \right)$.
b) Toạ độ vectơ $\vec{u}=2\overrightarrow{AB}-\overrightarrow{BC}$ là $\left( 4;0;3 \right)$.
c) Diện tích tam giác $OBC$ bằng 6.
d) Tứ giác $ABCD$ là hình bình hành khi toạ độ điểm $D\left( 1;1;1 \right)$.
Câu 4. Chi phí nhiên liệu của một chiếc tàu chạy trên sông được chia làm hai phần. Phần thứ nhất không phụ thuộc vào vận tốc và bằng 480 nghìn đồng trên 1 giờ. Phần thứ hai tỉ lệ thuận với lập phương của vận tốc, khi $v=10$ (km/giờ) thì phần thứ hai bằng 30 nghìn đồng/giờ.
a) Khi vận tốc $v=10$ (km/giờ) thì chi phí nguyên liệu cho phần thứ nhất trên $1\,\,km$ đường sông là 48000 đồng.
b) Khi vận tốc $v=30$ (km/giờ) thì tổng chi phí nguyên liệu trên $1\,\,km$ đường sông là 43000 đồng.
c) Hàm số xác định tổng chi phí nguyên liệu trên $1\,\,km$ đường sông với vận tốc $x\,\,(km/h)$ là $f(x)=\dfrac{480}{x}+0,03{{x}^{3}}$.
d) Vận tốc của tàu để tổng chi phí nguyên liệu trên $1\,\,km$ đường sông nhỏ nhất là $v=20$ (km/giờ).
Câu 1. Tính tổng hai giá trị cực trị của hàm số ${y=\dfrac{2{{x}^{2}}-x+1}{1-x}}$ ?
Câu 2. Một công ty uớc tính rằng tổng lợi nhuận $P$ cho một sản phẩm có thể được mô hình hoá bằng hàm số $P\left( x \right)=-{{x}^{3}}+450{{x}^{2}}+52500x$, trong đó $x$ là số lượng đơn vị sản phẩm đó được sản xuất và bán ra. Mức sản xuất nào sẽ mang lại lợi nhuận lớn nhất ?
Câu 3. Cho hàm số $y=\dfrac{3{{x}^{2}}+2x}{4x+4}.$ Tính khoảng cách từ điểm $M\left( 3;-2 \right)$ đến đường tiệm cận xiên của đồ thị hàm số này ?
Câu 4. Trong không gian ${Oxyz}$; cho ba điểm ${A\left( 1;2;-1 \right)}$, ${B\left( 2;1;1 \right)}$, ${C\left( 0;1;2 \right)}$. Gọi ${H}$ là trực tâm của tam giác ${ABC}$. Tính độ dài đoạn thẳng $OH$ (làm tròn đến hàng phần trăm) ?
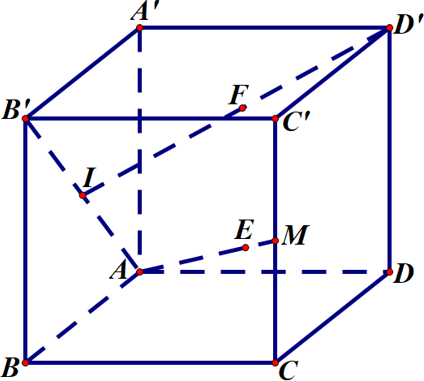
Câu 5. Bạn An đang nằm nghe nhạc trong phòng hình hộp chữ nhật, sàn nhà là hình vuông cạnh bằng 4 mét, chiều cao của phòng là 3,2 mét và phát hiện ra hai con nhện đang chăng tơ trong căn phòng của An, hai con nhện luôn di chuyển trên hai đường thẳng khác nhau. Giả sử căn phòng được mô hình hóa là hình hộp chữ nhật $ABCD.{A}'{B}'{C}'{D}'$ với $ABCD$ là nền phòng của An thì con nhện thứ nhất được coi như điểm $E$ di chuyển trên đường dây tơ nối từ đỉnh $A$ đến trung điểm $M$ của $C{C}'$, còn con nhện thứ hai được coi như điểm $F$ di chuyển trên đường dây tơ nối từ ${D}'$ đến tâm $I$ của mặt $AB{B}'{A}'$. Tính khoảng cách giữa hai con nhện khi đường thẳng đi qua hai con nhện vuông góc với trần nhà (đơn vị mét) ?
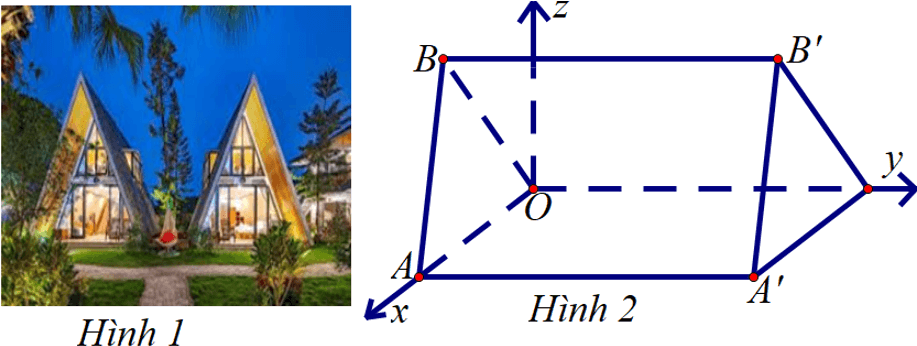
 Câu 6. Những căn nhà gỗ trong Hình 1 được phác thảo dưới dạng một hình lăng trụ đứng tam giác $OAB.{O}'{A}'{B}'$ như trong Hình 2. Với hệ trục toạ độ ${Oxyz}$ thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm ${A}'$ và ${B}'$ có tọa độ lần lượt là $\left( 240;450;0 \right)$ và $\left( 120;450;300 \right)$. Mỗi căn nhà gỗ có chiều dài là $a\text{ cm}$, chiều rộng là $b~\text{cm}$, mỗi cạnh bên của mặt tiền có độ dài là $c~\text{cm}$. Tính $a+b+c$ (làm tròn đến hàng đơn vị) ?
Câu 6. Những căn nhà gỗ trong Hình 1 được phác thảo dưới dạng một hình lăng trụ đứng tam giác $OAB.{O}'{A}'{B}'$ như trong Hình 2. Với hệ trục toạ độ ${Oxyz}$ thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm ${A}'$ và ${B}'$ có tọa độ lần lượt là $\left( 240;450;0 \right)$ và $\left( 120;450;300 \right)$. Mỗi căn nhà gỗ có chiều dài là $a\text{ cm}$, chiều rộng là $b~\text{cm}$, mỗi cạnh bên của mặt tiền có độ dài là $c~\text{cm}$. Tính $a+b+c$ (làm tròn đến hàng đơn vị) ?
 Giáo viên: Nguyễn Quốc Hoàn 0913661886 (hs.edu.vn)
Giáo viên: Nguyễn Quốc Hoàn 0913661886 (hs.edu.vn)_ _ _ _ _ _ Hết _ _ _ _ _ _
Thày cô, Học sinh tải về nếu hỏi mật khẩu thì nhập một trong các mk sau để mở file (NÊN copy và chú ý không dấu cách và không thừa khoảng trắng hay kí tự bất kì): hs.edu.vn https://hs.edu.vn/ https://edu365.edu.vn/ https://edu365.edu.vn edu365.edu.vn edu365free freeedu365 edu365.edu.vnfree edu365 hoc moi luc moi noi
(Nếu file quá nhiều lượt tải về trong ngày, xin bấm vào đây xem hướng dẫn để tải ngay)
Chúng tôi luôn mong nhận được sự đồng hành, góp ý và chia sẻ của thầy cô giáo và học sinh.
Xin gửi về địa chỉ:
Nhà giáo: Nguyễn Quốc Hoàn
Mobi, Zalo: 0913 661 886
Tel: 025 99 999 888 , 024 666 07 999 , 028 99 99 99 77
Giờ làm việc: 08h11 - 18h36 hàng ngày; trừ các ngày lễ và ngày thứ bẩy, chủ nhật.
Đánh giá và nhận xét
Đánh giá trung bình
(2 đánh giá)
5