Phát triển câu 50 đề tham khảo môn toán TN THPT năm 2023

Câu 1. Có bao nhiêu giá trị nguyên của tham số $a\in \left(-10;+\infty \right)$ để hàm số $y=\left|{{x}^{3}}+\left(a+2\right)x+9-{{a}^{2}}\right|$ đồng biến trên khoảng $\left(0;1\right)$?

A. 12.       B. 11.       C. 6.       D. 5.

Lời giải:

Xét $f\left(x\right)={{x}^{3}}+\left(a+2\right)x+9-{{a}^{2}}$,  $f'\left(x\right)=3{{x}^{2}}+a+2$

Để $y=\left|f\left(x\right)\right|$ đồng biến trên khoảng $\left(0;1\right)$

TH1: $\left\{\begin{align}&f'\left(x\right)\ge0,\forall x\in \left(0;1\right)\\ &f\left(0\right)\ge0\end{align}\right.$

$\Leftrightarrow \left\{ \begin{align}& 3{{x}^{2}}+a+2\ge 0,\forall x\in \left( 0;1 \right) \\ & 9-{{a}^{2}}\ge 0 \\ \end{align} \right.$  $\Leftrightarrow \left\{ \begin{align} & a\ge \underset{\left( 0;1 \right)}{\mathop{Max}}\,\left( -3{{x}^{2}}-2 \right) \\ & 9-{{a}^{2}}\ge 0 \\ \end{align} \right.$  $\Leftrightarrow \left\{ \begin{align}& a\ge -2 \\ & -3\le a\le 3 \\ \end{align} \right.$  $\Rightarrow a\in \left[ -2;3 \right]$

$a=\left\{-2;-1;0;1;2;3;\right\}$, có 6 giá trị

TH2: $\left\{\begin{align}&f'\left(x\right)\le,\forall x\in \left(0;1\right)\\ &f\left(0\right)\le0\end{align}\right.$

$\Leftrightarrow \left\{ \begin{align}  & 3{{x}^{2}}+a+2\le 0,\forall x\in \left( 0;1 \right) \\ & 9-{{a}^{2}}\le 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& 3{{x}^{2}}+a+2\le 0,\forall x\in \left( 0;1 \right) \\  & 9-{{a}^{2}}\le 0 \\ \end{align} \right.$ $\Rightarrow a\le -5$

Kết hợp với điều kiện bài toán $a=\left\{-9;-8;-7;-6;-5\right\}$, có 5 giá trị

Vậy có 11 giá trị thoả mãn.

Câu 2. Có bao nhiêu giá trị nguyên của tham số $m$ nhỏ hơn 10 để hàm số $y=\left|3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m\right|$ nghịch biến trến khoảng $\left(-\infty ;-1\right)$?

A. 3.       B. 4.       C. 5.       D. 6.

Lời giải:

Xét hàm số $f\left(x\right)=3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m\Rightarrow {f}'\left(x\right)=12{{x}^{3}}-12{{x}^{2}}-24x$

${f}'\left(x\right)=0\Leftrightarrow  \left[\begin{align}&x=-1\\ &x=0\\ &x=2\end{align}\right.$

BBT:

 

Hàm số $y=\left|f\left(x\right)\right|$ nghịch biến trên $\left(-\infty ;-1\right)\Leftrightarrow  m-5\ge0\Leftrightarrow  m\ge5$

Do yêu cầu $m$ là số nguyên nhỏ hơn 10 nên ta có $m\in \left\{5;6;7;8;9\right\}$

Vậy có 5 giá trị $m$ thỏa yêu cầu.

Câu 3. Có bao nhiêu giá trị nguyên của tham số $m$ thuộc $[-9;9]$ để hàm số $f(x)=\left|-\dfrac{1}{3}{{x}^{3}}+\dfrac{1}{2}(2m+3){{x}^{2}}-\left({{m}^{2}}+3m\right)x+\dfrac{2}{3}\right|$ nghịch biến trên khoảng $(1;2)$?

A. 3.       B. 2.       C. 16.       D. 9.

Lời giải:

Xét hàm số $g(x)=-\dfrac{1}{3}{{x}^{3}}+\dfrac{1}{2}(2m+3){{x}^{2}}-\left({{m}^{2}}+3m\right)x+\dfrac{2019}{2020}$ $\Rightarrow {g}'(x)=-{{x}^{2}}+(2m+3)x-\left({{m}^{2}}+3m\right)$

Để $f(x)$ nghịch biến trên khoảng $(1;2)$ ta xét hai trường hợp sau:

Trường hợp 1: $g(x)$ nghịch biến và không âm trên khoảng $(1;2)$.

Tức là $\left\{ \begin{array}{*{35}{l}}{g}'(x)\le 0,\forall x\in (1;2)  \\ g(2)\ge 0  \\\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}  -{{x}^{2}}+(2m+3)x-\left( {{m}^{2}}+3m \right)\le 0,\forall x\in (1;2)  \\ -\frac{1}{3}{{.2}^{3}}+\frac{1}{2}.(2m+3){{.2}^{2}}-\left( {{m}^{2}}+3m\right).2+\frac{2}{3}\ge 0  \\\end{array} \right.$  $\left\{ \begin{align}& x\ge m+3,\forall x\in (1;2) \\ & -2{{m}^{2}}-2m+4\ge 0 \\ \end{align} \right.$ hoặc $\left\{ \begin{align}  & x\le m,\quad \forall x\in (1;2) \\ & -2{{m}^{2}}-2m+4\ge 0 \\ \end{align} \right.$   Giải ra $m=-2$.

Trường hợp 2: $g(x)$ đồng biến và không dương trên khoảng $(1;2)$.

Tức là $\left\{ \begin{array}{*{35}{l}} {g}'(x)\ge 0,\forall x\in (1;2)  \\ g(2)\le 0  \\\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}-{{x}^{2}}+(2m+3)x-\left( {{m}^{2}}+3m \right)\ge 0,\forall x\in (1;2)  \\-\frac{1}{3}{{.2}^{3}}+\frac{1}{2}.(2m+3){{.2}^{2}}-\left( {{m}^{2}}+3m \right).2+\frac{2}{3}\le 0  \\\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}m\le x\le m+3,\forall x\in (1;2)  \\  -2{{m}^{2}}-2m+4\le 0  \\\end{array} \right.$ $\left\{ \begin{align}& m\ge 1 \\ & -1\le m\le 1 \\ \end{align} \right.$ hoặc $\left\{ \begin{align}  & m\le -2 \\ & -1\le m\le 1 \\ \end{align} \right.$  Giải ra $m=1$

Câu 4. Gọi $S$ là tập hợp các giá trị nguyên của $m$ sao cho hàm số $y=\left|-{{x}^{4}}+m{{x}^{3}}+2{{m}^{2}}{{x}^{2}}+m-1\right|$ đồng biến trên $\left(1;+\infty \right)$. Tổng tất cả các phần tử của $S$ bằng

A. $-1$.       B. $-2$.       C. 0.       D. 2.

Lời giải:

Gọi $g(x)=-{{x}^{4}}+m{{x}^{3}}+2{{m}^{2}}{{x}^{2}}+m-1$.

${g}'(x)=-4{{x}^{3}}+3m{{x}^{2}}+4{{m}^{2}}x=x\left(-4{{x}^{2}}+3mx+4{{m}^{2}}\right)=-4x\left(x-\dfrac{3-\sqrt{73}}{8}m\right)(x-\left.\dfrac{3+\sqrt{73}}{8}m\right)$

Gọi $a=\dfrac{3-\sqrt{73}}{8}m,b=\dfrac{3+\sqrt{73}}{8}m,b-a=\dfrac{2\sqrt{73}}{8}m$.

Nếu $m>0$ thì $b>a$, nếu $m<0$ thì $b<a$.

Ta có $\underset{x\to+\infty }{\mathop{\lim}}\,{g}'(x)=-\infty $ nên không xảy ra trường hợp hàm số $g(x)$ đồng biến trên khoảng $(1;+\infty )$

Để thỏa mãn yêu cầu đề bài thì phải có $g(x)$ nghịch biến trên $(1;+\infty )$ và $g(1)\le0$.

$g(1)\le0\Leftrightarrow  2{{m}^{2}}+2m-2\le0\Leftrightarrow  \dfrac{-1-\sqrt{5}}{2}\le m\le\dfrac{-1+\sqrt{5}}{2}$ (1).

$g(x)$ nghịch biến trên $(1;+\infty )\Leftrightarrow  {g}'(x)\le0,\forall x\in (1;+\infty )$ (2).

+) Nếu $m=0:{g}'(x)=-4{{x}^{3}}$. Điều kiện (1) và (2) đều thỏa mãn, do đó giá trị $m=0$ thỏa mãn yêu cầu đề bài.

$+)$ Nếu $0<m\le\dfrac{-1+\sqrt{5}}{2}$ (3): Dấu ${g}'(x)$ trên trục số như sau:

Để thỏa mãn điều kiện (2) thì $b=\dfrac{3+\sqrt{73}}{8}m\le1\Leftrightarrow  m\le\dfrac{-3+\sqrt{73}}{8}$ (4). Kết hợp (3) và (4) có: $0<m\le\dfrac{-1+\sqrt{5}}{2}$.

+ ) Nếu $\dfrac{-1-\sqrt{5}}{2}\le m<0$ (5): Dấu ${g}'(x)$ trên trục số như sau:

Để thỏa mãn điều kiện (2) thì $a=\dfrac{3-\sqrt{73}}{8}m\le1\Leftrightarrow  m\ge\dfrac{-3-\sqrt{73}}{8}$ (6). Kết hợp (5) và (6) có: $\dfrac{-3-\sqrt{73}}{8}\le m<0$.

Vậy các giá trị của ${m}$ thỏa mãn yêu cầu đề bài là $\dfrac{-3-\sqrt{73}}{8}\le m\le\dfrac{-1+\sqrt{5}}{2}$, suy ra các giá trị nguyên của $ {m}$ thỏa mãn yêu cầu đề bài là $m=-1,m=0$, do đó $S=-1$.

Câu 5. Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và $f(1)=1$. Đồ thị hàm số $y={f}'(x)$ như hình bên

 

Có bao nhiêu số nguyên dương $a$ để hàm số $y=|4f(\sin x)+\cos 2x-a|$ nghịch biến trên khoảng $\left(0;\dfrac{\pi}{2}\right)?$

A. 2.       B. 3.       C. 5.       D. Vô số.

Lời giải:

$y=|4f(\sin x)+\cos 2x-a|=\left|4f(\sin x)-2{{\sin }^{2}}x+1-a\right| {.}$

Đặt $t=\sin x\Rightarrow {{t}^{\prime}}=\cos x>0,x\in \left(0;\dfrac{\pi}{2}\right)$ nên khi $x$ tăng trên $\left(0;\dfrac{\pi}{2}\right)$ thì $t$ tăng trên $(0;1)$. Do đó hàm số $y=\left|4f(\sin x)-2{{\sin }^{2}}x+1-a\right|$ nghịch biến trên $\left(0;\dfrac{\pi}{2}\right)$ khi và chỉ khi hàm số $y=\left|4f(t)-2{{t}^{2}}+1-a\right|$ nghịch biến trên $(0;1)$.

Dễ thấy, điều kiện cần để hàm số $y=\left|4f(t)-2{{t}^{2}}+1-a\right|$ nghịch biến trên $(0;1)$ là phương trình $4f(t)-2{{t}^{2}}+1-a=0$ vô nghiệm trên $(0;1)$. (*)

Với điều kiện $(*),y=\left|4f(t)-2{{t}^{2}}+1-a\right|$ nghịch biến trên $(0;1)$ khi và chỉ khi ${y}'\le0,\forall t\in (0;1)\Leftrightarrow  \dfrac{\left(4{f}'(t)-4t\right)\left(4f(t)-2{{t}^{2}}+1-a\right)}{\left|4f(t)-2{{t}^{2}}+1-a\right|}\le0,\forall t\in (0;1).(**)$

Dựa vào đồ thị trên ta có ${f}'(t)<0,\forall t\in (0;1)$, do đó $4{f}'(t)-4t<0,\forall t\in (0;1)$.

Khi đó $(**)\Leftrightarrow  4f(t)-2{{t}^{2}}+1-a>0,\forall t\in (0;1)\Leftrightarrow  a<4f(t)-2{{t}^{2}}+1,\forall t\in (0;1)$  (điều kiện này luôn đảm bảo thỏa mãn $\left(*\right)$)

Hay $a\le4f(t)-2{{t}^{2}}+1,\forall t\in [0;1]\Leftrightarrow  a\le{{\min}_{[0;1]}}\left\{4f(t)-2{{t}^{2}}+1\right\}$.

Xét hàm số $g(t)=4f(t)-2{{t}^{2}}+1$ trên $[0;1]$có ${g}'(t)=4{f}'(t)-4t<0,\forall t\in [0;1]$, nên $g(t)$ nghịch biến trên $[0;1]$ $\Rightarrow {{\min}_{[0;1]}}g(t)=g(1)=3$

Vậy $a\le{{\min}_{[0;1]}}g(t)=3$.

Vì $a$ nguyên dương nên $0<a\le3\Rightarrow a\in \{1;2;3\}$.

Cách 2.

$y=|4f(\sin x)+\cos 2x-a|=\left|4f(\sin x)-2{{\sin }^{2}}x+1-a\right|$.

Đặt $t=\sin x\Rightarrow {t}'=\cos x>0,x\in \left(0;\dfrac{\pi}{2}\right)$ nên khi $x$ tăng trên $\left(0;\dfrac{\pi}{2}\right)$ thì $t$ tăng trên $(0;1)$.

Do đó hàm số $y=\left|4f(\sin x)-2{{\sin }^{2}}x+1-a\right|$ nghịch biến trên $\left(0;\dfrac{\pi}{2}\right)$ khi và chỉ khi hàm số $y=\left|4f(t)-2{{t}^{2}}+1-a\right|$ nghịch biến trên $(0;1)$.

Xét $g(t)=4f(t)-2{{t}^{2}}+1-a$ có $g(1)=4f(1)-2+1-a=3-a$. ${g}'(t)=4{f}'(t)-4t<0,\forall t\in (0;1)$.

Do đó $g(t)$ nghịch biến trên $(0;1)$.

Từ đây suy ra: $y=\left|4f(t)-2{{t}^{2}}+1-a\right|$ nghịch biến trên khoảng $(0;1)$ khi và chỉ khi $g(t)\ge0$ $,\forall t\in [0;1]$ hay $g(1)\ge0\Leftrightarrow  a\le3$.

Vì $a$ nguyên dương nên $a\in \{1;2;3\}$.

Câu 6. Có bao nhiêu số nguyên $m\in (-20;20)$ để hàm số $y=\left|3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m\right|$ nghịch biến trên khoảng $(-\infty ;-1)$.

A. 8.       B. 15.       C. 4.       D. 30.

Lời giải:

Xét hàm số $f(x)=3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m$

Ta có ${f}'(x)=12{{x}^{3}}-12{{x}^{2}}-24x=12x\left({{x}^{2}}-x-2\right)$.

${f}'(x)=0$ $\Leftrightarrow \left[ \begin{array}{*{35}{l}}x=0  \\x=-1.  \\  x=2  \\\end{array} \right.$ Dễ thấy $f'(x)<0,\,\,\forall x<-1$.

Lấy đối xứng đồ thị hàm số $f(x)$ qua trục hoành ta được đồ thị hàm số $\left|f(x)\right|$. Từ bảng biến thiên ta thấy hàm số $\left|f(x)\right|$ nghịch biến trên khoảng $(-\infty ;-1)\Leftrightarrow  m-5\ge0\Leftrightarrow  m\ge5$.

Vì $m$ nguyên và $m\in (-20;20)$ suy ra $m\in \{5;6;\ldots;17;18;19\}$.

Vậy có tất cả 15 giá trị nguyên của tham số $m$ thoả mãn yêu cầu bài toán.

Câu 7. Gọi $S$ là số giá trị $m$ nguyên thuộc khoảng $(-20;20)$ để đồ thị hàm số $y=\left|f(x)\right|=\left|2{{x}^{4}}-4(m+4){{x}^{3}}+3{{m}^{2}}{{x}^{2}}+48\right|$ đồng biến trên khoảng $(0;2)$. Phát biểu nào sau đây đúng?

A. $S$ chia hết cho 4.       B. $S$ chia cho 4 dư 1.       C. $S$ chia cho 4 dư 2.       D. $S$ chia cho 4 dư 3.

Lời giải:

Vì $f(0)=48>0$ nên hàm số $y=\left|f(x)\right|$ đồng biến trên khoảng $(0;2)$ khi và chỉ khi ${f}'(x)\ge$ $0,\forall x\in (0;2)$ $\Leftrightarrow  8{{x}^{3}}-12(m+4){{x}^{2}}+6{{m}^{2}}x\ge0,\forall x\in (0;2)$

$\Leftrightarrow  g(x)=4{{x}^{2}}-6(m+4)x+3{{m}^{2}}\ge0,\forall x\in (0;2)$

TH1: $ {\Delta }'\le 0$

TH2: $ \left\{ \begin{align}& {\Delta }'>0 \\ & g\left( 0 \right)\ge 0 \\  & g\left( 2 \right)\ge 0 \\ & \frac{S}{2}\ge 2 \\ \end{align} \right.$

TH3: $ \left\{ \begin{align}& {\Delta }'>0 \\ & g\left( 0 \right)\ge 0 \\ & g\left( 2 \right)\ge 0 \\  & \frac{S}{2}\le 0 \\ \end{align} \right.$

Giải ra $\left[ \begin{align}& m\ge \frac{6+2\sqrt{33}}{3} \\ & m\le \frac{6-2\sqrt{33}}{3} \\ \end{align} \right.$

$\Rightarrow m\in \{-19;-18;\ldots;-2\}\cup\{6;7;8;\ldots;19\}$, Suy ra $S=32$. Vậy $S$ chia hết cho 4.

Câu 8. Có bao nhiêu giá trị nguyên của tham số $a$ sao cho hàm số $y=\left|{{x}^{3}}-3{{x}^{2}}-ax+a\right|$ đồng biến trên khoảng $(0;+\infty )$?

A. 0.       B. 1.       C. 2.       D. Vô số.

Lời giải:

Đặt $f(x)={{x}^{3}}-3{{x}^{2}}-ax+a$.

Nhận xét: $f(x)=0$ có nghiệm ${{x}_{0}}\in (0;+\infty )$ thì hàm số $y=\left|f(x)\right|$ không thể đồng biến trên khoảng $(0;+\infty )$.

Suy ra $f(x)=0$ không có nghiệm trên khoảng $(0;+\infty )$.

Ta có ${f}'(x)=3{{x}^{2}}-6x-a$.

Khi đó $y=\left|{{x}^{3}}-3{{x}^{2}}-ax+a\right|=\left|f(x)\right|=\sqrt{{{f}^{2}}(x)}$ nên ${y}'=\dfrac{f\prime(x)\cdot f(x)}{\sqrt{{{f}^{2}}(x)}}$.

Hàm số đồng biến trên khoảng $(0 ;+\infty)$ khi và chỉ khi ${y}'\ge 0$ với $\forall x\in (0;+\infty )$ $ \Leftrightarrow \left\{ \begin{array}{*{35}{l}}  {f}'(x).f(x)\ge 0  \\f(x)\ne 0  \\\end{array} \right.$ , $ \forall x\in (0;+\infty )$  $ \Leftrightarrow \left\{ \begin{matrix}  f(x)>0  \\ {f}'(x)\ge 0  \\\end{matrix} \right.$ , vì $\underset{x\to +\infty }{\mathop{\lim }}\,f(x)=+\infty $.

$*\,\,\,f(x)>0,\forall x\in (0;+\infty )$.

Do ${f}'(x)\ge0,\forall x\in (0;+\infty )$ nên $f(x)>0,\forall x\in (0;+\infty )\Leftrightarrow  f(0)\ge0\Leftrightarrow  a\ge0$ (1).

* ${f}'(x)\ge0,\forall x\in (0;+\infty )\Leftrightarrow  3{{x}^{2}}-6x-a\ge0,\forall x\in (0;+\infty )$ $\Leftrightarrow  a\le\min\left(3{{x}^{2}}-6x\right),\forall x\in (0;+\infty )\Leftrightarrow  a\le-3$ (2).

Từ (1) và (2) suy ra không có giá trị $a$ nào thỏa mãn bài toán.

Câu 9. Cho hàm số $y=f(x)=\dfrac{1}{3}{{x}^{3}}-{{x}^{2}}+mx+2$. Có bao nhiêu giá trị nguyên của $m\in [-2020;2020]$ để hàm số $y=f\left(\left|x-2\right|\right)$ đồng biến trên $(-2;0)$?

A. 2020.       B. 2021.       C. 2012.       D. 2013.

Lời giải:

Xét hàm số $y=f(|x-2|)$ đồng biến trên $(-2;0)\Leftrightarrow  f(|x|)$ đồng biến trên $(-4;-2)$

Do đó $y=f(x)$ nghịch biến trên $(2;4)$.

Ta có ${f}'(x)={{x}^{2}}-2x+m\le0,\forall x\in (2;4)\Leftrightarrow  m\le-{{x}^{2}}+2x,\forall x\in (2;4)\Leftrightarrow  m\le-8$.

Do $m\in [-2020;2020]$ nên có 2013 giá trị nguyên của $m$.

Câu 10. Có bao nhiêu số nguyên $m$ thuộc khoảng $(-10;10)$ để hàm số $y=\left|2{{x}^{3}}-2mx+3\right|$ đồng biến trên $(1;+\infty )$?

A. 11.       B. 7.       C. 12.       D. 8.

Lời giải:

Xét hàm số: $f(x)=2{{x}^{3}}-2mx+3$ có: ${f}'(x)=6{{x}^{2}}-2m;\,\,{\Delta }'=12m$

+ Trường hợp 1: ${\Delta }'\le0\Leftrightarrow  m\le0$. Suy ra ${f}'(x)\ge0,\forall x\in (1;+\infty )$.

Vậy yêu cầu bài toán $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}m\le 0  \\f(1)\ge 0  \\ \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}m\le 0  \\  5-2m\ge 0  \\ \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}} m\le 0  \\m\le \frac{5}{2}  \\\end{array} \right.$ $\Leftrightarrow m\le 0$

Kết hợp với điều kiện $m\in \mathbb{Z};m\in (-10;10)$ ta được

$m\in $ $\{-9;-8;-7;-6;-5;-4;-3;-2;-1;0\}$

Ta có 10 giá trị của $m$ thoả mãn yêu cầu bài toán (1)

+ Trường hợp 2: ${\Delta }'>0\Leftrightarrow  m>0$. Suy ra ${f}'(x)=0$ có 2 nghiệm phân biệt ${{x}_{1}},{{x}_{2}}\left({{x}_{1}}<{{x}_{2}}\right)$

Ta có bảng biến thiên:

Vậy yêu cầu bài toán $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}  m>0  \\{{x}_{1}}<{{x}_{2}}\le 1  \\f(1)\ge 0  \\\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}m>0  \\-\frac{2m}{6}+1\ge 0  \\ 5-2m\ge 0  \\\end{array} \right.$ $\Leftrightarrow 0<m\le \frac{5}{2}$

Kết hợp với điều kiện $m\in \mathbb{Z};m\in (-10;10)$ ta được $m\in \{1;2\}$.

Ta có 2 giá trị của $m$ thoả mãn yêu cầu bài toán (2).

Từ (1) và (2) suy ra: có tất cả có 12 giá trị của $m$ thoả mãn yêu cầu bài toán.

Câu 11. Có bao nhiêu giá trị nguyên của tham số $m$ số hàm số $f(x)=\left|{{x}^{3}}-3{{x}^{2}}+mx+10\right|$ đồng biến trên khoảng $(-1;1)$?

A. 6.       B. 3.       C. 4.       D. 5.

Lời giải:

Xét hàm số $f(x)={{x}^{3}}-3{{x}^{2}}+mx+10$, có đạo hàm ${f}'(x)=3{{x}^{2}}-6x+m$.

Hàm số $y=\left|f\left(x\right)\right|$ đồng biến trên khoảng $(-1;1)$ thì bảng biến thiên của hàm số $y=f(x)$ trong khoảng $(-1;1)$ phải có hình dạng như sau:

Trường hợp 1: Hàm số $f(x)$ đồng biến trên khoảng $(-1;1)$ và không âm trên $(-1;1)$ tức là $\left\{ \begin{array}{*{35}{l}} f(-1)\ge 0  \\{f}'(x)\ge 0,\forall x\in (-1;1)  \\\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}6-m\ge 0  \\m\ge 6x-3{{x}^{2}},\forall x\in (-1;1)  \\\end{array} \right.$  $\Leftrightarrow \left\{ \begin{array}{*{35}{l}} m\le 6  \\ m\ge 3  \\\end{array} \right.$ $\Leftrightarrow 3\le m\le 6$

Trường hợp 2: Hàm số $f(x)$ nghịch biến trên khoảng $(-1;1)$ và không dương trên $(-1;1)$ tức là $ \left\{ \begin{array}{*{35}{l}}f(-1)\le 0  \\{f}'(x)\le 0,\forall x\in (-1;1)  \\\end{array} \right.$  $ \Leftrightarrow \left\{ \begin{array}{*{35}{l}}6-m\le 0  \\m\le 6x-3{{x}^{2}},\forall x\in (-1;1)  \\\end{array} \right.$  $ \Leftrightarrow \left\{ \begin{array}{*{35}{l}}m\ge 6  \\m\le -9  \\\end{array} \right.$  $ \Leftrightarrow m\in \varnothing $.

Kết hợp với điều kiện ta được kết quả $m\in \{3,4,5,6\}$.

Vây có 4 giá trị nguyên của tham số $m$.

Câu 12. Cho hàm số $f(x)=\left|{{x}^{3}}-(2m-5)x+2018\right|$. Có bao nhiêu giá trị nguyên của tham số $m$ thuộc $[-2019;2019]$ để hàm số đồng biến trên khoảng $(1;3)$?

A. 3032.       B. 4039.      C. 0.      D. 2021.

Lời giải:

Xét hàm số $f(x)={{x}^{3}}-(2m-5)x+2018$, có đạo hàm $f(x)=3{{x}^{2}}-(2m-5)$.

Hàm số $y=\left|f(x)\right|$ đồng biến trên khoảng $(1;3)$ thì đồ thì của hàm số trong khoảng

$(1;3)$ phải có hình dạng như sau:

 

Trường hợp 1: Hàm số $f(x)$ đồng biến trong khoảng $(1;3)$ và không âm trên $(1;3)$ tức là $\left\{ \begin{array}{*{35}{l}}  f(1)\ge 0  \\ {f}'(x)\ge 0\forall x\in (1;3)  \\\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}  2m\le 3{{x}^{2}}+5,\forall x\in (1;3)  \\  2024-2m\ge 0  \\ \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}m\le 4  \\ m\le 1012  \\\end{array} \right.$ $\Leftrightarrow m\le 4$

Trường hợp 2: Hàm số $f(x)$ nghịch biến trong khoảng $(1;3)$ và không dương trên $(1;3)$ tức là  $\left\{ \begin{array}{*{35}{l}}f(1)\le 0  \\{{f}^{\prime }}(x)\le 0\forall x\in (1;3)  \\ \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}2m\ge 3{{x}^{2}}+5\forall x\in (1;3)  \\2024-2m\le 0  \\ \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}} m\ge 4  \\m\ge 1012  \\\end{array} \right.$ $\Leftrightarrow m\ge 1012$

Kết hợp với điều kiện ta được kết quả $m\in [-2019;4]\cup[1012;2019]$. Vậy có 3032 giá trị của $m$.

Câu 13. Tất cả các giá trị của tham số $m$ để hàm số $y=\left|m{{x}^{3}}-m{{x}^{2}}+16x-32\right|$ nghịch biến trên khoảng $\left(1;\,2\right)$ là

A. $-1\le m\le2$.       B. $-2\le m\le0$.       C. $m\in \varnothing $.       D. $m\in \mathbb{R}$.

Lời giải:

Đặt $f\left(x\right)=m{{x}^{3}}-m{{x}^{2}}+16x-32$

$y=\left|f\left(x\right)\right|=\left\{\begin{align}&f\left(x\right) với f\left(x\right)\ge0\\ &-f\left(x\right) với f\left(x\right)<0\end{align}\right.$ $\Rightarrow {y}'=\left\{\begin{align}&{f}'\left(x\right) với f\left(x\right)>0\\ &-{f}'\left(x\right) với f\left(x\right)<0\end{align}\right.$

Trường hợp 1. $\left\{\begin{align}&{f}'\left(x\right)\le0\quad\forall x\in \left(1;\,2\right)\\ &f\left(2\right)\ge0\end{align}\right.$

$\Leftrightarrow \left\{ \begin{align}& 3m{{x}^{2}}-2mx+16\le 0\ \in \forall x\in \left( 1;\,2 \right) \\ & 8m-4m\ge 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& m\left( 3{{x}^{2}}-2x \right)\le -16\ \forall x\in \left( 1;\,2 \right) \\ & m\ge 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & m\le \frac{-16}{3{{x}^{2}}-2x} \\ & m\ge 0 \\\end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & m\le -16 \\ & m\ge 0 \\ \end{align} \right.$ $\Leftrightarrow m\in \varnothing $.

Trường hợp 2. $\left\{\begin{align}&{f}'\left(x\right)\ge0\quad\forall x\in \left(1;\,2\right)\\ &f\left(2\right)\le0\end{align}\right.$

$\Leftrightarrow \left\{ \begin{align}& 3m{{x}^{2}}-2mx+16\ge 0\ \in \forall x\in \left( 1;\,2 \right) \\ & 8m-4m\le 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& m\ge \frac{-16}{3{{x}^{2}}-2x}\ \forall x\in \left( 1;\,2 \right) \\ & m\le 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}  & m\ge -2 \\  & m\le 0 \\ \end{align} \right.$ $\Leftrightarrow -2\le m\le 0$.

Vậy với $-2\le m\le0$ hàm số $y=\left|m{{x}^{3}}-m{{x}^{2}}+16x-32\right|$ nghịch biến trên khoảng $\left(1;\,2\right)$.

Câu 14. Có bao nhiêu giá trị nguyên của tham số $a\in \left(-23;23\right)$ để hàm số $y=\left|{{x}^{4}}-2{{x}^{2}}+\left(a+1\right)x+{{a}^{2}}-4\right|$ đồng biến trên khoảng $\left(0;1\right)$?

A. 32.       B. 24.       C. 23.       D. 22.

Lời giải:

Xét $f\left(x\right)={{x}^{4}}-2{{x}^{2}}+\left(a+1\right)x+{{a}^{2}}-4$

$f'\left(x\right)=4{{x}^{3}}-4x+a+1$

Để $y=\left|f\left(x\right)\right|$ đồng biến trên khoảng $\left(0;1\right)$

Trường hợp 1. $\left\{\begin{align}&f'\left(x\right)\ge0,\forall x\in \left(0;1\right)\\ &f\left(0\right)\ge0\end{align}\right.$

$\Leftrightarrow \left\{ \begin{align} & 4{{x}^{3}}-4x+a+1\ge 0,\forall x\in \left( 0;1 \right) \\& {{a}^{2}}-4\ge 0 \\ \end{align} \right.$ $\Leftrightarrow $ $\left\{ \begin{align}& a\ge \underset{\left( 0;1 \right)}{\mathop{max}}\,\left( -4{{x}^{3}}+4x-1 \right) \\ & a\le -2 \\\end{align} \right.$ hoặc $\left\{ \begin{align}& a\ge \underset{\left( 0;1\right)}{\mathop{max}}\,\left( -4{{x}^{3}}+4x-1 \right) \\  & a\ge 2 \\ \end{align} \right.$ $\Leftrightarrow $ $\left\{ \begin{align}& a\ge \frac{-9+8\sqrt{3}}{9} \\  & a\le -2 \\ \end{align} \right.$ hoặc $\left\{ \begin{align}& a\ge \frac{-9+8\sqrt{3}}{9} \\  & a\ge 2 \\ \end{align} \right.$  Tìm ra $a\ge 2$

Trường hợp 2. $\left\{\begin{align}&f'\left(x\right)\le0,\forall x\in \left(0;1\right)\\ &f\left(0\right)\le0\end{align}\right.$

$\Leftrightarrow \left\{ \begin{align}& 4{{x}^{3}}-4x+a+1\le 0,\forall x\in \left( 0;1 \right) \\ & {{a}^{2}}-4\le 0 \\ \end{align} \right.$  $\Leftrightarrow \left\{ \begin{align}& a\le \underset{\left( 0;1 \right)}{\mathop{\min }}\,\left( -4{{x}^{3}}+4x-1 \right) \\  & -2\le a\le 2 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& a\le -1 \\ & -2\le a\le 2 \\ \end{align} \right.$ $\Leftrightarrow -2\le a\le -1$

Vậy có 23 giá trị thoả mãn.

Câu 15. Có bao nhiêu giá trị nguyên âm của tham số $m$ để hàm số $y=\left|{{x}^{5}}+2{{x}^{4}}-m{{x}^{2}}+3x-20\right|$ nghịch biến trên $\left(-\infty ;-2\right)$?

A. 4.       B. 6.       C. 7.       D. 9.

Lời giải:

Xét hàm số $f\left(x\right)={{x}^{5}}+2{{x}^{4}}-m{{x}^{2}}+3x-20$

${f}'\left(x\right)=5{{x}^{4}}+8{{x}^{3}}-2mx+3$

Ta thấy $\underset{x\to-\infty }{\mathop{\lim}}\,f\left(x\right)=-\infty $ nên hàm số $y=\left|f\left(x\right)\right|$ nghịch biến trên $\left(-\infty ;-2\right)$ khi và chỉ khi hàm số $y=f\left(x\right)$ đồng biến trên $\left(-\infty ;-2\right)$ và hàm số không dương trên miền $\left(-\infty ;-2\right)$

$\Leftrightarrow \left\{ \begin{align}& {f}'\left( x \right)\ge 0\forall x\in \left( -\infty ;-2 \right) \\ & f\left( -2 \right)\le 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& 5{{x}^{4}}+8{{x}^{3}}-2mx+3\ge 0\forall x\in \left( -\infty ;-2 \right) \\  & -4m-26\le 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& 5{{x}^{3}}+8{{x}^{2}}+\frac{3}{x}\le 2m\forall x\in \left( -\infty ;-2 \right) \\  & m\ge -\frac{13}{2} \\ \end{align} \right.$

Xét hàm số $g\left(x\right)=5{{x}^{3}}+8{{x}^{2}}+\dfrac{3}{x}$ trên $\left(-\infty ;-2\right)$

${g}'\left(x\right)=15{{x}^{2}}+16x-\dfrac{3}{{{x}^{2}}}={{\left(2x+4\right)}^{2}}+11{{x}^{2}}-16-\dfrac{3}{{{x}^{2}}}$

Ta có ${{\left(2x+4\right)}^{2}}>0, {}11{{x}^{2}}>44, {}\dfrac{3}{{{x}^{2}}}<\dfrac{3}{4} {}\forall x\in \left(-\infty ;-2\right)$

Suy ra $g'(x)>0+44-16-\frac{3}{4}>0,\,\,\forall x\in \left( -\infty ;-2 \right)$

Ta có $5{{x}^{3}}+8{{x}^{2}}+\dfrac{3}{x}\le2m {}\forall x\in \left(-\infty ;-2\right)\Leftrightarrow  -\dfrac{19}{2}\le2m\Leftrightarrow  m\ge-\dfrac{19}{4}.$

Kết hợp với $m\ge-\dfrac{13}{2}$ ta có $m\ge-\dfrac{19}{4}.$ Do đó $m\in \left\{-4;-3;-2;-1\right\}$

Suy ra có 4 giá trị nguyên âm thỏa mãn đề bài.

Câu 16. Tổng tất cả các giá trị nguyên của tham số $m$ trong đoạn $\left[-10;10\right]$ để hàm số $y=\left|\dfrac{mx+3}{x+m+2}\right|$ đồng biến trên $\left(1;\,+\infty \right)$ bằng

A. 55.       B. 54.       C. 5.       D. 3.

Lời giải:

Xét hàm số $y=\dfrac{mx+3}{x+m+2}$ với $x\ne -m-2$, có $y'=\dfrac{{{m}^{2}}+2m-3}{{{\left(x+m+2\right)}^{2}}}$.

Hàm số $y=\left|\dfrac{mx+3}{x+m+2}\right|$đồng biến trên $\left(1;\,+\infty \right)$ khi xảy ra một trong hai trường hợp sau :

Trường hợp 1: $\left\{\begin{array}{l}y^{\prime}=\frac{m^2+2 m-3}{(x+m+2)^2}>0 \\y(1) \geq 0 \\-m-2 \notin(1 ;+\infty)\end{array}, \forall x>1 \Leftrightarrow\left\{\begin{array} { c } { m ^ { 2 } + 2 m - 3 > 0 } \\{ \frac { m + 3 } { m + 3 } \geq 0 } \\{ - m - 2 \leq 1 }\end{array} \Leftrightarrow \left\{\begin{array}{l}{\left[\begin{array}{c}m<-3 \\m>1\end{array}\right.} \\m \geq-3\end{array}\Leftrightarrow m>1\right.\right.\right.$

Trường hợp 2: $\left\{\begin{array}{l}y^{\prime}=\frac{m^2+2 m-3}{(x+m+2)^2}<0 \\ y(1) \leq 0 \\ -m-2 \notin(1 ;+\infty)\end{array}, \forall x>1 \Leftrightarrow\left\{\begin{array}{c}m^2+2 m-3<0 \\ \frac{m+3}{m+3} \leq 0 \\ -m-2 \leq 1\end{array} \Leftrightarrow m \in \varnothing\right.\right.$

Từ kết quả trên ta có  $m\in \left(1\,;\,+\infty \right)$, mà $\left\{\begin{align}m\in \mathbb{Z}\\ &m\in \left[-10\,;10\right]\end{align}\right.$ suy ra $m\in \left\{2\,;\,3\,;\,4\,;\,5\,;6\,;7\,;8\,;9\,;10\right\}$.

Vậy $S=54$.

Câu 17. Cho hàm số $f(x)=\ln ^3 x+6(m-1) \ln ^2 x-3 m^2 \ln x+4$. Biết rằng đoạn [a, b] là tập hợp tất cả các giá trị của tham số $m$ để hàm số $y=|f(x)|$ đồng biến trên khoảng $(e,+\infty)$. Giá trị biểu thức $a+3 b$ bằng

A. $4+\sqrt{6}$.       B. $12+2 \sqrt{6}$.       C. 4.       D. 3.

Lời giải:

Đặt $t=\ln x$ là hàm số đồng biến trên khoảng $(0 ;+\infty)$ và $x \in(e,+\infty) \rightarrow t \in(1 ;+\infty)$.

Xét hàm số $g(t)=t^3+6(m-1) t^2-3 m^2 t+4$ trên khoảng $(1 ;+\infty)$.

Ta có: $g^{\prime}(t)=3 t^2+12(m-1) t-3 m^2$ và $\lim _{t \rightarrow+\infty} g(t)=+\infty$

Hàm số $y=|g(t)|$ đồng biến trên khoảng $(1 ;+\infty) \Leftrightarrow\left\{\begin{array}{l}g^{\prime}(t) \geq 0, \forall t \in[1 ;+\infty)(1) \\ g(1) \geq 0\end{array}\right.$

$+(2) \Rightarrow-3 m^2+6 m-1 \geq 0 \Rightarrow \frac{3-\sqrt{6}}{3} \leq m \leq \frac{3+\sqrt{6}}{3}$

$+\Delta_{g^{\prime}}=36(m-1)^2+9 m^2>0, \forall m \rightarrow g^{\prime}(t)$ luôn có 2 nghiệm $t_1, t_2$

${(1) }\Rightarrow {{t}_{2}}=-2(m-1)+\sqrt{5{{m}^{2}}-8m+4}\le 1\Leftrightarrow \sqrt{5{{m}^{2}}-8m+4}\le 2m-1$

$\Leftrightarrow \left\{ \begin{array}{*{35}{l}}2m-1\ge 0  \\ 5{{m}^{2}}-8m+4\le 4{{m}^{2}}-4m+1  \\ \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}2m-1\ge 0  \\ {{m}^{2}}-4m+3\le 0  \\\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{*{35}{l}}m\ge \frac{1}{2}  \\ 1\le m\le 3  \\\end{array} \right.$ $\Leftrightarrow 1\le m\le 3.$

Kết hợp (1) và (2) ta được $m \in\left[1 ; \frac{3+\sqrt{6}}{3}\right] \Rightarrow a=1 ; b=\frac{3+\sqrt{6}}{3}$.

Vậy $a+3 b=4+\sqrt{6}$.

Câu 18. Cho hàm số bậc ba $y=f\left(x\right)$ có đồ thị như hình vẽ

 

Số giá trị nguyên của tham số $m$ thuộc đoạn $\left[-10;10\right]$ để hàm số $g\left(x\right)=\left|f\left(f\left(x\right)\right)-2f\left(x\right)+m\right|$ đồng biến trên $\left(0;1\right)$ là

A. 8.       B. 7.       C. 19.       D. 20.

Lời giải:

Đặt $h\left(x\right)=f\left(f\left(x\right)\right)-2f\left(x\right)+m$$\Rightarrow {h}'\left(x\right)={f}'\left(x\right)\left[{f}'\left(f\left(x\right)\right)-2\right]$

Ta thấy ${f}'\left(x\right)\le0,\forall x\in \left(0;1\right)$

$\forall x\in \left(0;1\right)\Rightarrow f\left(x\right)\in \left(-1;1\right)\Rightarrow {f}'\left(f\left(x\right)\right)-2\le0,\forall x\in \left(0;1\right)$

$\Rightarrow {h}'\left(x\right)\ge0,\forall x\in \left(0;1\right)$

Để hàm số đồng biến trên $\left(0;1\right)$ $\Rightarrow h\left(0\right)\ge0\Leftrightarrow  f\left(f\left(0\right)\right)-2f\left(0\right)+m\ge0$

$\Leftrightarrow  f\left(1\right)-2+m\ge0\Leftrightarrow  m\ge3$. Khi đó có 8 giá trị nguyên của tham số $m$ thuộc đoạn $\left[-10;10\right]$ để hàm số đồng biến trên $\left(0;1\right)$.

Câu 19. Có bao nhiêu giá trị nguyên của tham số $a\in \left[-30;30\right]$ để hàm số $y=\left|{{x}^{4}}-{{x}^{2}}+\left(a-3\right)x+9-{{a}^{2}}\right|$ nghịch biến trên khoảng $\left(1;2\right)$?

A. 26.       B. 34.       C. 27.       D. 25.

Lời giải:

Xét $f\left(x\right)={{x}^{4}}-{{x}^{2}}+\left(a-3\right)x+9-{{a}^{2}}$

${f}'\left(x\right)=4{{x}^{3}}-2x+a-3$

Để $y=\left|f\left(x\right)\right|$ nghịch biến trên khoảng $\left(1;2\right)$

TH1:$\left\{\begin{align}&f'\left(x\right)\ge0,\forall x\in \left(1;2\right)\\ &f\left(2\right)\le0\end{align}\right.$

$\Leftrightarrow \left\{ \begin{align}& 4{{x}^{3}}-{{x}^{2}}+a-3\ge 0,\forall x\in \left( 1;2 \right) \\ & -{{a}^{2}}+2a+15\le 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& a\ge \underset{\left( 1;2 \right)}{\mathop{max}}\,\left( -4{{x}^{3}}+{{x}^{2}}+3 \right) \\ & -{{a}^{2}}+2a+15\le 0 \\ \end{align} \right.$  $\Leftrightarrow \left\{ \begin{align}& a\ge 0 \\  & a\le -3 \\ \end{align} \right.$ hoặc $\left\{ \begin{align}& a\ge 0 \\ & a\ge 5 \\ \end{align} \right.$ $\Leftrightarrow a\ge 5$

Kết hợp với điều kiện bài toán $a\in \left\{5;6;...;29;30\right\}$, 26 giá trị

TH2: $\left\{\begin{align}&f'\left(x\right)\le0,\forall x\in \left(1;2\right)\\ &f\left(2\right)\ge0\end{align}\right.$

$\Leftrightarrow \left\{ \begin{align}& 4{{x}^{3}}-{{x}^{2}}+a-3\le 0,\forall x\in \left( 1;2 \right) \\ & -{{a}^{2}}+2a+15\ge 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& a\le \underset{\left( 1;2 \right)}{\mathop{\min }}\,\left( -4{{x}^{3}}+{{x}^{2}}+3 \right) \\ & -{{a}^{2}}+2a+15\ge 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& a\le -25 \\ & -3\le a\le 5 \\ \end{align} \right.$ $\Leftrightarrow a\in \varnothing $

Vậy có 26 giá trị thoả mãn.

Câu 20. Có bao nhiêu giá trị nguyên của tham số $m\in \left(-10;10\right)$ để hàm số $y=\left|{{x}^{3}}+3{{x}^{2}}-\left({{m}^{2}}-3m+2\right)x+9-{{m}^{2}}\right|$ đồng biến trên khoảng $\left(0;1\right)$?

A. 12.       B. 14.       C. 6.       D. 5.

Lời giải:

Xét $f\left(x\right)={{x}^{3}}+3{{x}^{2}}-\left({{m}^{2}}-3m+2\right)x+9-{{m}^{2}}$

$f'\left(x\right)=3{{x}^{2}}+6x-\left({{m}^{2}}-3m+2\right)$

Để $y=\left|f\left(x\right)\right|$ đồng biến trên khoảng $\left(0;1\right)$

Ÿ Trường hợp 1: $\left\{\begin{align}&f'\left(x\right)\ge0,\forall x\in \left(0;1\right)\\ &f\left(0\right)\ge0\end{align}\right.$

$\Leftrightarrow \left\{ \begin{align}& 3{{x}^{2}}+6x-\left( {{m}^{2}}-3m+2 \right)\ge 0,\forall x\in \left( 0;1 \right) \\ & 9-{{m}^{2}}\ge 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & {{m}^{2}}-3m+2\le \underset{\left( 0;1 \right)}{\mathop{Min}}\,\left( 3{{x}^{2}}+6x \right) \\ & 9-{{m}^{2}}\ge 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& {{m}^{2}}-3m+2\le 0 \\ & -3\le m\le 3 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& 1\le m\le 2 \\ & -3\le m\le 3 \\\end{align} \right.$ $\Rightarrow m\in \left[ 1;2 \right]$

Vì $m\in \mathbb{Z}\Rightarrow m\in \left\{ 1;2 \right\}$có 2 giá trị.

Ÿ Trường hợp 2: $\left\{\begin{align}&f'\left(x\right)\le0,\forall x\in \left(0;1\right)\\ &f\left(0\right)\le0\end{align}\right.$

$\Leftrightarrow \left\{ \begin{align}& 3{{x}^{2}}+6x-\left( {{m}^{2}}-3m+2 \right)\le 0,\forall x\in \left( 0;1 \right) \\ & 9-{{m}^{2}}\ge 0 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & {{m}^{2}}-3m+2\ge \underset{\left( 0;1 \right)}{\mathop{Max}}\,\left( 3{{x}^{2}}+6x \right) \\ & 9-{{m}^{2}}\le 0 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& m\le -3 \\ & m\ge \frac{3+\sqrt{37}}{2} \\ \end{align} \right.$

Vì $m\in \mathbb{Z}\Rightarrow $ $m\in \left\{-9;-8;-7;-6;-5;-4;-3;5;6;7;8;9\right\}$: có 12 giá trị.

Vậy có 14 giá trị thoả mãn yêu cầu đề bài.

Câu 21. Có bao nhiêu số nguyên $m$ để hàm số $y\,=\,\left|x\sqrt{x-1}\,+\,\left(2m-3\right)\sqrt{x-1}\,+\,16\,-\,{{m}^{2}}\right|$ đồng biến trên khoảng $\left(1;\,+\infty \right)$ ?

A. 1.       B. 2.       C. 3.       D. 4.

Lời giải:

Ta có: $y\,=\,\left|x\sqrt{x-1}\,+\,\left(2m-3\right)\sqrt{x-1}\,+\,16\,-\,{{m}^{2}}\right|$$=\,\left|\left(x-1\right)\sqrt{x-1}\,+2\,\left(m-1\right)\sqrt{x-1}\,+\,16\,-\,{{m}^{2}}\right|$

Đặt $\sqrt{x-1}=t$. Với $x\in \left(1;\,+\infty \right)$ thì $t\in \left(0;\,+\infty \right)$.

Khi đó yêu cầu bài toán trở thành: Tìm số giá trị nguyên của $m$ để hàm số $y=\,\left|{{t}^{3}}\,+2\,\left(m-1\right)t\,+\,16\,-\,{{m}^{2}}\right|$ đồng biến trên khoảng $t\in \left(0;\,+\infty \right)$.

Xét $f\left(t\right)\,=\,{{t}^{3}}\,+2\,\left(m-1\right)t\,+\,16\,-\,{{m}^{2}}$.

Ta có ${f}'\left(t\right)\,=\,3{{t}^{2}}\,+\,2m-2.\,$${f}'\left(t\right)\,=\,0\,\Leftrightarrow  \,{{t}^{2}}\,=\,\dfrac{2-2m}{3}.$

+) Trường hợp 1: Nếu $2-\,2m\,>\,0\,\Leftrightarrow  \,m\,<\,1$ thì phương trình ${f}'\left(t\right)\,=\,0$ có hai nghiệm phân biệt ${{t}_{1}}\,<\,0\,\,<\,{{t}_{2}}.$ Khi đó luôn tồn tại $\left(a;b\right)\,\subset\,\left(0;\,+\infty \right)$ sao cho hàm số $y\,=\,\left|f\left(x\right)\right|\,$nghịch biến trên $\left(a;b\right).$ Suy ra $m\,<\,1$ không thỏa mãn.

+) Trường hợp 2: Nếu $2-\,2m\,\,\le\,\,0\,\Leftrightarrow  \,m\,\,\ge\,\,1$ thì ${f}'\left(t\right)\,\ge\,0\,,\forall t\in \mathbb{R}$. Do đó $y\,=\,\left|f\left(t\right)\right|\,$ đồng biến trên $\left(0;\,+\infty \right)$ khi $\left\{ \begin{align}& m\ge 1 \\ & f\left( 0 \right)\ge 0 \\ \end{align} \right.$  $\left\{ \begin{align}& m\ge 1 \\ & 16-{{m}^{2}}\ge 0 \\ \end{align} \right.$ $\Leftrightarrow 1\le m\le 4.$

Vì $m\,\in \,\mathbb{Z}\,$nên $m\,\,\in \,\left\{1,2,\,\,3,\,\,4\right\}.$.

Câu 22. Cho hàm số $y=f\left(x\right)={{x}^{3}}-3{{x}^{2}}+2$. Hỏi có bao nhiêu giá trị nguyên của tham số $m\in \left[-10;10\right]$ để hàm số $g\left(x\right)=f\left(\left|x+m\right|\right)$ nghịch biến trên $\left(0;1\right)$?

A. 7.       B. 8.       C. 9.       D. 10.

Lời giải:

Ta có ${f}'\left(x\right)=3{{x}^{2}}-6x=3x\left(x-2\right)$

Xét hàm số $g\left(x\right)=f\left(\left|x+m\right|\right)$ có

${g}'\left(x\right)={f}'\left(\left|x+m\right|\right).\dfrac{x+m}{\left|x+m\right|}=\dfrac{x+m}{\left|x+m\right|}.3\left|x+m\right|.\left(\left|x+m\right|-2\right)=3\left(x+m\right).\left(\left|x+m\right|-2\right)$

${g}'\left(x\right)=0\Leftrightarrow  \left[\begin{align}&x=-m-2\\ &x=-m+2\end{align}\right.$

${g}'\left(x\right)$ không xác định khi $x=-m$.

Ta có bảng biến thiên của hàm số $g\left(x\right)$ như sau

Dựa vào bảng biến thiên ta có hàm số nghịch biến trên khoảng $\left(0;1\right)$

$\left[ \begin{align}& \left( 0;1 \right)\subset \left( -\infty ;-m-2 \right) \\ & \left( 0;1 \right)\subset \left( -m;-m+2 \right) \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& 1\le -m-2 \\ & -m\le 0<1\le -m+2 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& m\le -3 \\ & 0\le m\le 1 \\ \end{align} \right.$

Mà $m\in \left[-10;10\right]$ nên có 10 giá trị nguyên của $m$ thỏa mãn đề bài.

Câu 23. Cho hàm số $f\left(x\right)$ có đạo hàm trên $\mathbb{R}$, biết $f\left(0\right)=0$ và đồ thị hàm số $y={f}'\left(x\right)$ như hình sau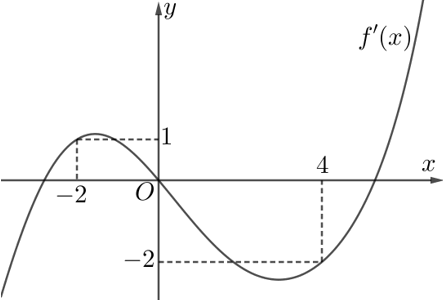

Hàm số $g\left(x\right)=\left|4f\left(x\right)+{{x}^{2}}\right|$ đồng biến trên khoảng nào dưới đây?

A. $\left(4;+\infty \right)$.       B. $\left(0;4\right)$.       C. $\left(-\infty ;-2\right)$.       D. $\left(-2;0\right)$.

Lời giải:

Xét hàm số $h\left(x\right)=4f\left(x\right)+{{x}^{2}}$ trên $\mathbb{R}$

${h}'\left(x\right)=4{f}'\left(x\right)+2x$

${h}'\left(x\right)=0\Leftrightarrow  {f}'\left(x\right)=-\dfrac{1}{2}x$

Vẽ đường thẳng $y=-\dfrac{1}{2}x$ vào đồ thị trên, dựa vào sự tương giao của đồ thị hàm số $y={f}'\left(x\right)$ và đường thẳng $y=-\dfrac{1}{2}x$, ta có ${h}'\left(x\right)=0\Leftrightarrow  x\in \left\{-2;0;4\right\}$

Suy ra bảng biến thiên của hàm số $h\left(x\right)$ như sau: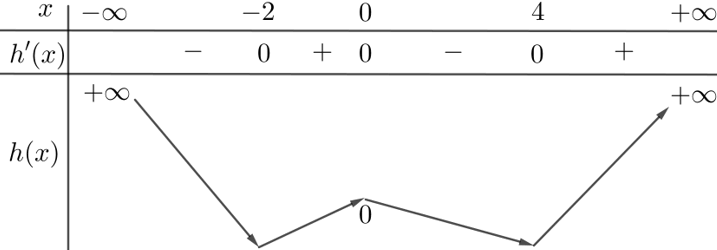

Từ đó ta có bảng biến thiên của hàm số $g\left(x\right)=\left|h\left(x\right)\right|$ như sau:

 

Dựa vào bảng biến thiên trên, ta thấy hàm số $g\left(x\right)$ đồng biến trên khoảng $\left(0;4\right)$.

Câu 24. Cho hàm số $f\left(x\right)$ liên tục trên $\mathbb{R}$ có đồ thị hàm số $y={f}'\left(x\right)$ như hình sau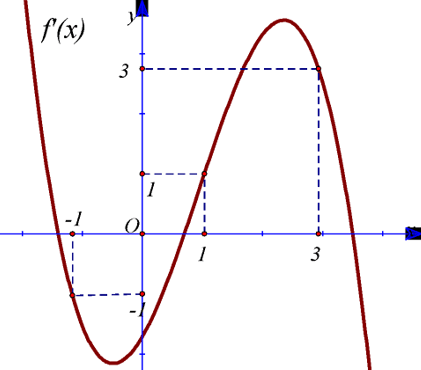

Hàm số $g\left(x\right)=2f\left(\left|x-1\right|\right)-{{x}^{2}}+2 {x}+2020$ đồng biến trên khoảng nào dưới đây?

A. $\left(0;1\right)$.       B. $\left(-3;1\right)$.       C. $\left(1;3\right)$.       D. $\left(-2;0\right)$.

Lời giải:

Ta có $g\left(x\right)=2f\left(\left|x-1\right|\right)-{{x}^{2}}+2x+2020=2f\left(\left|x-1\right|\right)-{{\left|x-1\right|}^{2}}+2021$

$\Rightarrow {g}'\left(x\right)=\left[2{f}'\left(\left|x-1\right|\right)-2\left|x-1\right|\right].\dfrac{x-1}{\left|x-1\right|}$ với mọi $x\ne 1$

${g}'\left(x\right)=0\Leftrightarrow  {f}'\left(\left|x-1\right|\right)=\left|x-1\right|$

Ta vẽ đường thẳng $y=x$ cắt đồ thị hàm số $y={f}'\left(x\right)$ tại các điểm $x=-1, {}x=1, {}x=3$.

Dựa vào đồ thị của hai hàm số trên ta có ${f}'\left( \left| x-1 \right| \right)=\left| x-1 \right|$ $\Leftrightarrow \left[ \begin{align}& \left| x-1 \right|=-1 \\ & \left| x-1 \right|=1 \\ & \left| x-1 \right|=3 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& x=0 \\ & x=2 \\ & x=-2 \\ & x=4 \\ \end{align} \right.$.

Lập bảng biến thiên của hàm số $g\left(x\right)$ ta có

Dựa vào bảng biến thiên ta có hàm số $g\left(x\right)$ đồng biến trên khoảng $\left(0;1\right).$

Câu 25. Cho hàm số $y=f\left(x\right)$. Đồ thị hàm số $y={f}'\left(x\right)$ như hình vẽ sau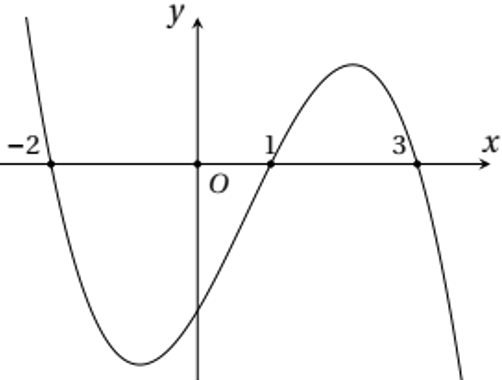

Hàm số $g\left(x\right)=f\left(\left|4-2x\right|\right)$ nghịch biến trên khoảng nào sau đây?

A. $\left(\dfrac{1}{2};\dfrac{3}{2}\right)$.       B. $\left(-\infty ;-2\right)$.       C. $\left(\dfrac{5}{2};7\right)$.       D. $\left(\dfrac{3}{2};\dfrac{5}{2}\right)$.

Lời giải:

Với $x\le2$. Khi đó $g\left(x\right)=f\left(4-2x\right)$.

Ta có ${g}'\left(x\right)=-2{f}'\left(4-2x\right)$, ${g}'\left( x \right)<0\Leftrightarrow {f}'\left( 4-2x \right)>0$ $\Leftrightarrow \left[ \begin{align} & 4-2x<-2 \\ & 1<4-2x<3 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& x>3 \\ & \frac{1}{2}<x<\frac{3}{2} \\ \end{align} \right.$

So điều kiện $x\le2$ ta được $g\left(x\right)$ nghịch biến trên $\left(\dfrac{1}{2};\dfrac{3}{2}\right)$.

Với $x>2.$ Khi đó $g\left(x\right)=f\left(2x-4\right)$.

Ta có ${g}'\left(x\right)=2{f}'\left(2x-4\right)$, ${g}'\left( x \right)<0\Leftrightarrow {f}'\left( 2x-4 \right)<0$ $\Leftrightarrow \left[ \begin{align} & -2<2x-4<1 \\ & 2x-4>3 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& 1<x<\frac{5}{2} \\ & x>\frac{7}{2} \\ \end{align} \right.$

So điều kiện $x>2$ ta được $g\left(x\right)$ nghịch biến trên $\left(2;\dfrac{5}{2}\right)$ và $\left(\dfrac{7}{2};+\infty \right)$.

Câu 26. Cho hàm số $y=f\left(x\right)$ có đồ thị của hàm số $y={f}'\left(x\right)$ như hình vẽ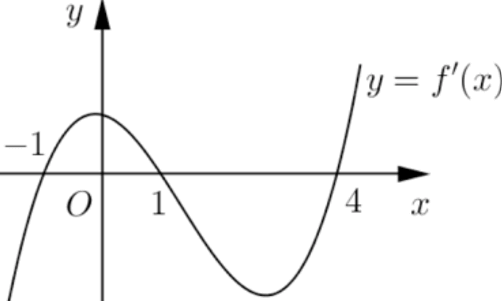

Hàm số $y=f\left(\left|{{x}^{2}}-3\right|\right)$ nghịch biến trên khoảng nào dưới đây?

A. $\left(-\infty ;-2\right)$.       B. $\left(-2;-\dfrac{7}{4}\right)$.       C. $\left(0;\dfrac{3}{2}\right)$.       D. $\left(2;3\right)$.

Lời giải:

Chú ý: ${{\left(\left|x\right|\right)}^{\prime}}=\dfrac{x}{\left|x\right|}\Rightarrow {{\left(\left|u\right|\right)}^{\prime}}=\dfrac{{u}'.u}{\left|u\right|}$

$y=f\left(\left|{{x}^{2}}-3\right|\right)\Rightarrow {y}'=\dfrac{2x\left({{x}^{2}}-3\right)}{\left|{{x}^{2}}-3\right|}.{f}'\left(\left|{{x}^{2}}-3\right|\right)$

${y}'=0$ $\Leftrightarrow \left[ \begin{align}& x=0 \\ & {{x}^{2}}-3=\pm 1 \\ & {{x}^{2}}-3=4 \\\end{align} \right.$ và $x\ne \pm \sqrt{3}$  $\Leftrightarrow \left[ \begin{array}{*{35}{l}} x=0  \\x=\pm 2  \\x=\pm \sqrt{2}  \\ x=\pm \sqrt{7}  \\\end{array} \right.$ và $x\ne \pm \sqrt{3}$

${y}'$ không xác định tại $x=\pm \sqrt{3}$.

Ta có bảng xét dấu sau

Suy ra hàm số nghịch biến trên khoảng $\left(-2;-\dfrac{7}{4}\right)$.

Câu 27. Cho hàm số bậc bốn $y=f\left(x\right)$ và $f\left(1\right)=0.$ Biết hàm số $y={f}'\left(x\right)$ có đồ thị như hình vẽ bên

 

Hàm số $g\left(x\right)=\left|f\left(1-\dfrac{x}{2}\right)-\dfrac{{{x}^{2}}}{8}\right|$ đồng biến trên khoảng nào dưới đây?

A. $\left(-\infty ;-4\right).$       B. $\left(4;+\infty \right).$       C. $\left(2;4\right).$       D. $\left(-3;-1\right).$

Lời giải:

Xét hàm số $h(x)=f\left(1-\dfrac{x}{2}\right)-\dfrac{{{x}^{2}}}{8}$

Ta có ${h}'\left(x\right)=-\dfrac{1}{2}{f}'\left(1-\dfrac{x}{2}\right)-\dfrac{x}{4}=0\Leftrightarrow  -\dfrac{1}{2}\left({f}'\left(1-\dfrac{x}{2}\right)+\dfrac{x}{2}\right)=0$ $\left(3\right)$

Đặt $1-\dfrac{x}{2}=t\Rightarrow \dfrac{x}{2}=1-t$

Khi đó $\left( 3 \right)\Leftrightarrow {f}'\left( t \right)-\left( t-1 \right)=0$ $\Leftrightarrow \left[ \begin{align}& t=-1 \\ & t=1 \\ & t=3 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& x=4 \\ & x=0 \\ & x=-4 \\ \end{align} \right.$

Ta có bảng biến thiên của hàm số là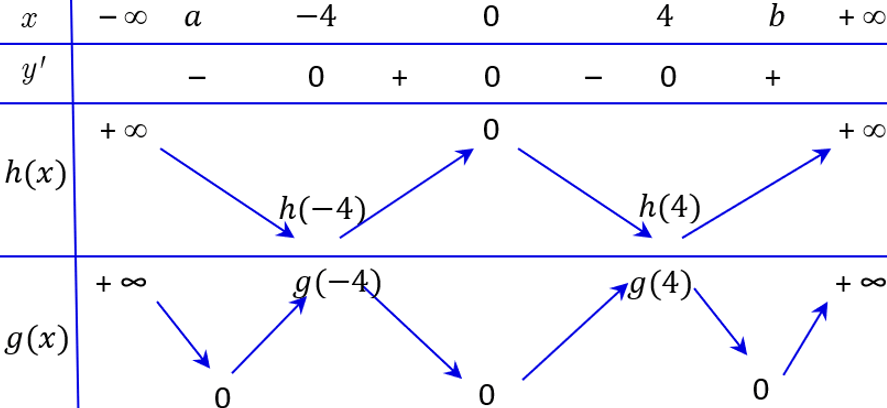

Dễ thấy ${h}'\left(2\right)=-\dfrac{1}{2}\left({f}'\left(0\right)+1\right)<0$

$h\left(0\right)=f\left(1\right)=0$

Từ đó ta có hàm số đồng biến trên $\left(2;4\right)$.

Câu 28. Cho hàm số $f\left(x\right)={{x}^{4}}+2{{x}^{2}}+1$. Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $g\left(x\right)=f\left(3\left|x-m\right|+{{m}^{2}}\right)$ đồng biến trên $\left(5;+\infty \right)$?

A. 2.       B. 3.       C. 5.       D. Vô số.

Lời giải:

Ta có ${f}'\left(x\right)=4{{x}^{3}}+4x=0\Leftrightarrow  x=0$

$g\left(x\right)=f\left(3\left|x-m\right|+{{m}^{2}}\right)\Rightarrow {g}'\left(x\right)=\dfrac{3\left(x-m\right)}{\left|x-m\right|}.{f}'\left(3\left|x-m\right|+{{m}^{2}}\right)$

${g}'\left( x \right)=0$ $\Leftrightarrow \left[ \begin{array}{*{35}{l}}x\ne m  \\x=m\text{ }(loai)  \\3\left| x-m \right|+{{m}^{2}}=0\left( VN \right)  \\\end{array} \right.$

${g}'\left(x\right)$ không xác định tại $x=m.$

Ta có bảng xét dấu sau

 

Để hàm số đồng biến trên $\left(5;+\infty \right)$ $\Rightarrow m\le5\Rightarrow $ Có 5 giá trị nguyên dương của $m$.

Câu 29. Cho hàm số $f\left(x\right)=\,{{x}^{4}}+2{{x}^{2}}+1$. Có bao nhiêu giá trị nguyên của tham số $m\in \left[0\,;\,10\right]$ để hàm số $g\left(x\right)=f\left(3\left|x-m\right|+{{m}^{2}}\right)$ nghịch biến trên $\left(-\infty \,;\,1\right)$?

A. 8.       B. 9.       C. 10.       D. 11.

Lời giải:

Xét hàm số $f\left(x\right)=\,{{x}^{4}}+2{{x}^{2}}+1$

Ta có ${f}'\left(x\right)=4{{x}^{3}}+4x$; ${f}'\left(x\right)=0\Leftrightarrow  x=0$

Bảng biến thiên

Ta có ${g}'\left(x\right)={f}'\left(3\left|x-m\right|+{{m}^{2}}\right).{{\left(3\left|x-m\right|+{{m}^{2}}\right)}^{\prime}}$ =${f}'\left(3\left|x-m\right|+{{m}^{2}}\right).\dfrac{3\left(x-m\right)}{\left|x-m\right|}$.

${g}'\left(x\right)=0\Leftrightarrow  \left[\begin{align}&x-m=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left(1\right)\\ &3\left|x-m\right|+{{m}^{2}}=0\,\,\,\left(2\right)\end{align}\right.$

TH1: Nếu $m=0$ $\Rightarrow $ phương trình ${g}'\left(x\right)=0\Leftrightarrow  x=0$$\Rightarrow $ không thỏa mãn nghịch biến trên khoảng $\left(-\infty \,;\,1\right)$ nên trường hợp này bị loại.

TH2: Nếu $m>0$ $\Rightarrow $ phương trình ${g}'\left(x\right)=0\Leftrightarrow  x=m$

Ta có $3\left|x-m\right|+{{m}^{2}}>0\,\,\forall x<1$ $\Rightarrow {f}'\left(3\left|x-m\right|+{{m}^{2}}\right)>0\,\,\forall \,x\in \left(-\infty \,;\,1\right)$ nên ${g}'\left(x\right)<0\Leftrightarrow  x<m$.

$\Rightarrow $ hàm số $y=g\left(x\right)$ nghịch biến trên $\left(-\infty \,;\,1\right)$ $\Leftrightarrow  {g}'\left(x\right)<0\,\forall \,x\in \left(-\infty \,;\,1\right)$ $\Leftrightarrow  \,\left(-\infty \,;\,1\right)\subset\left(-\infty \,;\,m\right)\Leftrightarrow  1\le m$ $\Rightarrow m\in \left\{1;2;3;4\,;5;6;7;8;9;10\right\}$. Nên có 10 giá trị thỏa mãn.

Câu 30. Cho hàm số $y=f\left(x\right)$. Biết rằng hàm số $y={f}'\left(x\right)$ có đồ thị như hình vẽ bên dưới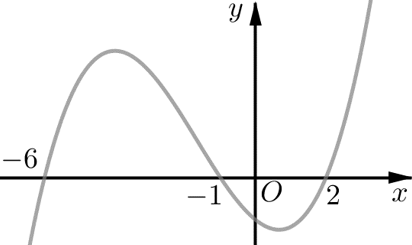

Hàm số $y=f\left(3-{{x}^{2}}\right)$ đồng biến trên khoảng

A. $\left(0;1\right)$.       B. $\left(-1;0\right)$.       C. $\left(2;3\right)$.       D. $\left(-2;-1\right)$.

Lời giải:

Cách 1:

Đặt $y=g\left(x\right)=f\left(3-{{x}^{2}}\right)$.

Ta có: ${g}'\left(x\right)=-2x.{f}'\left(3-{{x}^{2}}\right)$.

${g}'\left(x\right)=0\Leftrightarrow  -2x.{f}'\left(3-{{x}^{2}}\right)=0$ $\Leftrightarrow  \left[\begin{align}&x=0\\ &{f}'\left(3-{{x}^{2}}\right)=0\end{align}\right.$ $\Leftrightarrow  \left[\begin{align}&x=0\\ &3-{{x}^{2}}=-6\\ &3-{{x}^{2}}=-1\\ &3-{{x}^{2}}=2\end{align}\right.$ $\Leftrightarrow  \left[\begin{align}&x=0\\ &x=\pm 3\\ &x=\pm 2\\ &x=\pm 1\end{align}\right.$.

Bảng xét dấu của ${g}'\left(x\right)$:

Suy ra hàm số $y=f\left(3-{{x}^{2}}\right)$ đồng biến trên mỗi khoảng: $\left(-3;-2\right),\,\,\left(-1;0\right),\,\,\left(1;2\right),\,\,\left(3;+\infty \right)$.

Vậy hàm số $y=f\left(3-{{x}^{2}}\right)$ đồng biến trên khoảng $\left(-1;0\right)$.

Cách 2:

Dựa vào đồ thị của $y={f}'\left(x\right)$ ta chọn $y={f}'\left(x\right)=\left(x+6\right)\left(x+1\right)\left(x-2\right)$.

Đặt $y=g\left(x\right)=f\left(3-{{x}^{2}}\right)$.

Ta có: ${g}'\left(x\right)=-2x.{f}'\left(3-{{x}^{2}}\right)=-2x\left(9-{{x}^{2}}\right)\left(4-{{x}^{2}}\right)\left(1-{{x}^{2}}\right)$.

${g}'\left(x\right)=0$ $\Leftrightarrow  \left[\begin{align}&x=0\\ &x=\pm 3\\ &x=\pm 2\\ &x=\pm 1\end{align}\right.$.

Bảng xét dấu của ${g}'\left(x\right)$:

Suy ra hàm số $y=f\left(3-{{x}^{2}}\right)$ đồng biến trên mỗi khoảng: $\left(-3;-2\right),\,\,\left(-1;0\right),\,\,\left(1;2\right),\,\,\left(3;+\infty \right)$.

Vậy hàm số $y=f\left(3-{{x}^{2}}\right)$ đồng biến trên khoảng $\left(-1;0\right)$.

Câu 31. Cho hàm số bậc bốn $y=f(x)$ có đồ thị của hàm số $y={f}'(x)$ như hình vẽ bên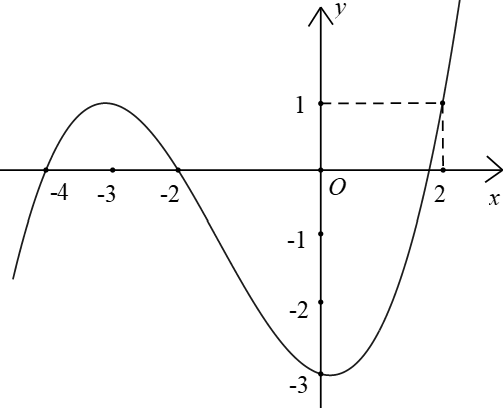

Hàm số $y=3f(x)+{{x}^{3}}-6{{x}^{2}}+9x$ đồng biến trên khoảng nào trong các khoảng sau đây?

A. $\left(0;2\right)$.       B. $\left(-1;1\right)$.       C. $\left(1;+\infty \right)$.       D. $\left(-2;0\right)$.

Lời giải:

Hàm số $f(x)=a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+e,(a\ne 0)$; ${f}'(x)=4a{{x}^{3}}+3b{{x}^{2}}+2cx+d$.

Đồ thị hàm số $y={f}'(x)$ đi qua các điểm $(-4;0),(-2;0),(0;-3),(2;1)$ nên ta có:

$\left\{ \begin{align}& -256a+48b-8c+d=0 \\ & -32a+12b-4c+d=0 \\ & d=-3 \\ & 32a+12b+4c+d=1 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& a=\frac{5}{96} \\ & b=\frac{7}{24} \\ & c=-\frac{7}{24} \\ & d=-3 \\ \end{align} \right.$

Do đó hàm số $y=3f(x)+{{x}^{3}}-6{{x}^{2}}+9x;{y}'=3\left({f}'(x)+{{x}^{2}}-4x+3\right)=3\left(\dfrac{5}{24}{{x}^{3}}+\dfrac{15}{8}{{x}^{2}}-\dfrac{55}{12}x\right)$

${y}'=0\Leftrightarrow  \left[\begin{align}&x=-11\\ &x=0\\ &x=2\end{align}\right.$. Hàm số đồng biến trên các khoảng $(-11;0)$ và $\left(2;+\infty \right)$.

Câu 32. Cho hàm số $f\left(x\right)$ có đạo hàm trên $\mathbb{R}$ là ${f}'\left(x\right)=\left(x-1\right)\left(x+3\right)$. Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $\left[-10;20\right]$ để hàm số $y=f\left({{x}^{2}}+3x-m\right)$ đồng biến trên khoảng $\left(0;2\right)$?

A. 16.       B. 17.       C. 18.       D. 20.

Lời giải:

Ta có ${y}'={f}'\left({{x}^{2}}+3x-m\right)=\left(2x+3\right){f}'\left({{x}^{2}}+3x-m\right)$.

Theo đề bài ta có: ${f}'\left(x\right)=\left(x-1\right)\left(x+3\right)$

Suy ra ${f}'\left(x\right)>0\Leftrightarrow  \left[\begin{align}&x<-3\\ &x>1\end{align}\right.$ và ${f}'\left(x\right)<0\Leftrightarrow  -3<x<1$.

Hàm số đồng biến trên khoảng $\left(0;2\right)$ khi ${y}'\ge0,\forall x\in \left(0;2\right)$

$\Leftrightarrow  \left(2x+3\right){f}'\left({{x}^{2}}+3x-m\right)\ge0,\forall x\in \left(0;2\right)$.

Do $x\in \left(0;2\right)$ nên $2x+3>0,\forall x\in \left(0;2\right)$. Do đó, ta có:

${y}'\ge 0,\forall x\in \left( 0;2 \right)$ $\Leftrightarrow {f}'\left( {{x}^{2}}+3x-m \right)\ge 0$ $\Leftrightarrow \left[ \begin{align}& {{x}^{2}}+3x-m\le -3 \\ & {{x}^{2}}+3x-m\ge 1 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& m\ge {{x}^{2}}+3x+3 \\ & m\le {{x}^{2}}+3x-1 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& m\ge \underset{\left[ 0;2 \right]}{\mathop{\max }}\,\left( {{x}^{2}}+3x+3 \right) \\ & m\le \underset{\left[ 0;2 \right]}{\mathop{\min }}\,\left( {{x}^{2}}+3x-1 \right) \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align} & m\ge 13 \\  & m\le -1 \\ \end{align} \right.$.

Do $m\in \left[-10;20\right]$, $m\in \mathbb{Z}$ nên có 18 giá trị nguyên của $m$ thỏa yêu cầu đề bài.

Câu 33. Cho hàm số $f\left(x\right)$. Hàm số $y={f}'\left(x\right)$ có đồ thị như hình sau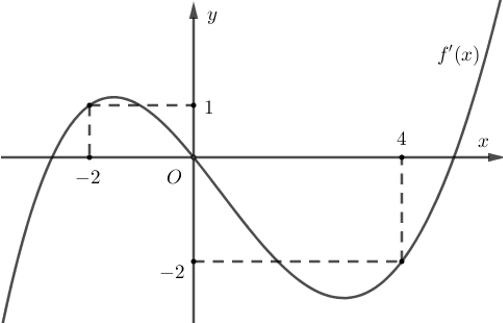

Có tất cả bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $g(x)=4f(x-m)+{{x}^{2}}-2mx+2020$ đồng biến trên khoảng $(1;2).$

A. 0.       B. 1.       C. 2.       D. 3.

Lời giải:

Ta có $g'(x)=4f'(x-m)+2x-2m$

$g'(x)\ge0\Leftrightarrow  f'(x-m)\ge-\dfrac{x-m}{2\,\,}\,\,\,(*)$

Đặt $t=x-m$ thì $(*)\Leftrightarrow  f'(t)\ge-\dfrac{t}{2}$

Vẽ đường thẳng $y=-\dfrac{x}{2}$ trên cùng hệ trục $Oxy$ với đồ thị $y={f}'\left(x\right)$.

Từ đồ thị ta có $f'(t)\ge -\frac{t}{2}$ $\Leftrightarrow \left[ \begin{align}& -2\le t\le 0 \\ & t\ge 4 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& m-2\le x\le m \\ & x\ge m+4 \\ \end{align} \right.$

Hàm số $g(x)$ đồng biến trên khoảng $(1;2)\Leftrightarrow $$g'(x)\ge 0\,\,\,\forall x\in \left( 1;2 \right)$

$\Leftrightarrow \left[ \begin{align}& m-2\le 1<2\le m \\ & m+4\le 1 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& 2\le m\le 3 \\ & m\le -3 \\ \end{align} \right.$

Vì $m$ nguyên dương nên $m\in \left\{2;3\right\}.$

Vậy có hai giá trị nguyên dương của $m$ để hàm số $g(x)$ đồng biến trên khoảng $(1;2).$

Câu 34. Cho hai hàm số $f\left(x\right)$ và $g\left(x\right)$ xác định và liên tục trên $\mathbb{R}$. Đồ thị $y={f}'\left(2x-1\right)$ như hình vẽ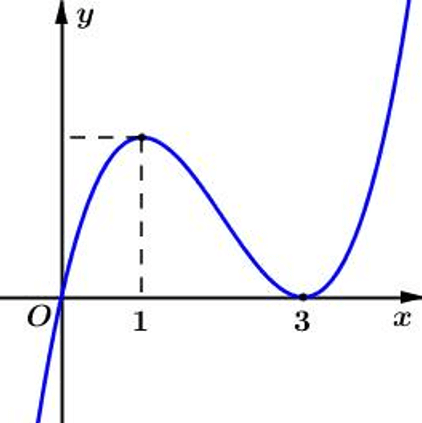

Có bao nhiêu số nguyên $m\in \left[-10;10\right]$ để $g\left(x\right)=f\left({{x}^{2}}+m\right)$ đồng biến trên khoảng $\left(1;+\infty \right)$.

A. 11.       B. 12.       C. 13.       D. 14.

Lời giải:

Xét $y={f}'\left(2x-1\right)=ax{{\left(x-3\right)}^{2}},\,\,a>0$. Đặt $t=2x-1\Rightarrow x=\dfrac{t+1}{2}$.

Ta có $y={f}'\left(t\right)=a\left(\dfrac{t+1}{2}\right){{\left(\dfrac{t+1}{2}-3\right)}^{2}}=\dfrac{1}{8}a\left(t+1\right){{\left(t-5\right)}^{2}}$.

Suy ra ${g}'\left(x\right)=2.x.{f}'\left({{x}^{2}}+m\right)=\dfrac{1}{4}ax\left({{x}^{2}}+m+1\right){{\left({{x}^{2}}+m-5\right)}^{2}}$.

Để hàm số $g\left(x\right)=f\left({{x}^{2}}+m\right)$ đồng biến trên $\left(1;+\infty \right)\Leftrightarrow  {g}'\left(x\right)\ge0,\,\forall x\in \left(1;+\infty \right)$

$\Leftrightarrow  \dfrac{1}{4}ax\left({{x}^{2}}+m+1\right){{\left({{x}^{2}}+m-5\right)}^{2}}\ge0,\,\forall x\in \left(1;+\infty \right)\Leftrightarrow  {{x}^{2}}+m+1\ge0,\,\forall x\in \left(1;+\infty \right)$

$\Leftrightarrow  {{x}^{2}}\ge-m-1,\,\forall x\in \left(1;+\infty \right)\Leftrightarrow  1\ge-m-1\Leftrightarrow  m\ge-2$.

Vậy $m\in \left\{-2;-1;0;1;2;3;4;5;6;7;8;9;10\right\}$ nên có 13 giá trị $m$ thỏa mãn.

Câu 35. Cho hàm số $y=f\left(x\right)$ liên tục trên $\mathbb{R}$, biết $f\left(2\right)=4.$ Biết hàm số $y={f}'\left(x\right)$ có đồ thị như hình vẽ sau

 

Hàm số $g\left(x\right)=\left|f\left(2x-4\right)-2{{x}^{2}}+8x-10\right|$ đồng biến trên khoảng nào dưới đây?

A. $\left(-\infty ;1\right).$       B. $\left(1;3\right).$       C. $\left(3;4\right).$       D. $\left(4;+\infty \right).$

Lời giải:

Xét hàm số $h(x)=f\left(2x-4\right)-2{{x}^{2}}+8x-10$

Ta có ${h}'\left(x\right)=2{f}'\left(2x-4\right)-4x+8=0=2\left({f}'\left(2x-4\right)-\left(2x-4\right)\right)=0$ $\left(3\right)$

Đặt $t=2x-4$

Khi đó (3) ${f}'\left( t \right)=t$ $\Leftrightarrow \left[ \begin{align}& t=-2 \\ & t=2 \\ & t=4 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& x=1 \\ & x=3 \\ & x=4 \\ \end{align} \right.$

Ta có bảng biến thiên của hàm số là

Dễ thấy ${h}'\left(2\right)=2{f}'\left(0\right)>0$

$h\left(3\right)=f\left(2\right)-18+24-10=0$

Từ đó ta có hàm số đồng biến trên $\left(3;4\right)$.

Câu 36. Cho hàm số $y=f\left(x\right)$ có đạo hàm $f'\left(x\right)={{x}^{2}}+2x-3,\forall x\in \mathbb{R}.$ Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $\left[-10;20\right]$ để hàm số $g\left(x\right)=f\left({{x}^{2}}+3x-m\right)+{{m}^{2}}+1$ đồng biến trên $\left(0;2\right)?$

A. 16.       B. 17.       C. 18.       D. 19.

Lời giải:

Ta có $f'\left(t\right)={{t}^{2}}+2t-3\ge0\Leftrightarrow  \left[\begin{align}&t\le-3\\ &t\ge1\end{align}\right.\,\,\,\left(*\right).$

Có $g'\left(x\right)=\left(2x+3\right)f'\left({{x}^{2}}+3x-m\right)$

Vì $2x+3>0,\forall x\in \left(0;2\right)$ nên $g\left(x\right)$ đồng biến trên $\left(0;2\right)\Leftrightarrow  g'\left(x\right)\ge0,\forall x\in \left(0;2\right)$

$\Leftrightarrow  f'\left({{x}^{2}}+3x-m\right)\ge0,\forall x\in \left(0;2\right)$

$\Leftrightarrow \left[ \begin{align}& {{x}^{2}}+3x-m\le -3,\forall x\in \left( 0;2 \right) \\ & {{x}^{2}}+3x-m\ge 1,\forall x\in \left( 0;2 \right) \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& {{x}^{2}}+3x\le m-3,\forall x\in \left( 0;2 \right) \\ & {{x}^{2}}+3x\ge m+1,\forall x\in \left( 0;2 \right) \\ \end{align} \right.$

Có $h\left(x\right)={{x}^{2}}+3x$ luôn đồng biến trên $\left(0;2\right)$ nên từ  $\Rightarrow \left[ \begin{align}& m-3\ge 10 \\ & m+1\le 0 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& m\ge 13 \\ & m\le -1 \\ \end{align} \right.$

Vì $\left\{\begin{align}&m\in \left[-10;20\right]\\ &m\in \mathbb{Z}\end{align}\right.\Rightarrow $ Có 18 giá trị của tham số $m$.

Vậy có 18 giá trị của tham số $m$ cần tìm.

Câu 37. Cho hàm số $y=f\left(x\right)$ có đạo hàm liên tục trên $\mathbb{R}$ và có đồ thị $y={f}'\left(x\right)$ như hình vẽ bên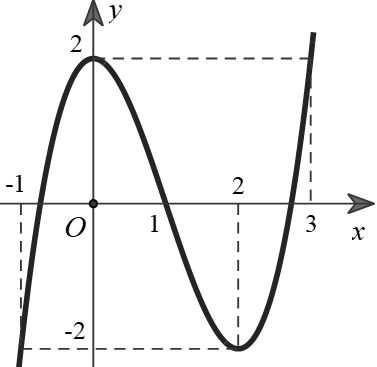

Đặt $g\left(x\right)=f\left(x-m\right)-\dfrac{1}{2}{{\left(x-m-1\right)}^{2}}+2019$, với $m$ là tham số thực. Gọi $S$ là tập hợp các giá trị nguyên dương của $m$ để hàm số $y=g\left(x\right)$ đồng biến trên khoảng $\left(5;6\right)$. Tổng tất cả các phần tử trong $S$ bằng:

A. 4.       B. 11.       C. 14.       D. 20.

Lời giải:

Ta có ${g}'\left(x\right)={f}'\left(x-m\right)-\left(x-m-1\right)$

Cho ${g}'\left(x\right)=0\Leftrightarrow  {f}'\left(x-m\right)=x-m-1$

Đặt $x-m=t\Rightarrow f'\left(t\right)=t-1$

Khi đó nghiệm của phương trình là hoành độ giao điểm của đồ thị hàm số $y={f}'\left(t\right)$ và và đường thẳng $y=t-1$, vẽ các đồ thị trên cùng một hệ trục.

Dựa vào đồ thị hàm số ta có được ${f}'\left(t\right)=t-1\Leftrightarrow  \left[\begin{align}&t=-1\\ &t=1\\ &t=3\end{align}\right.$

Bảng xét dấu của ${g}'\left(t\right)$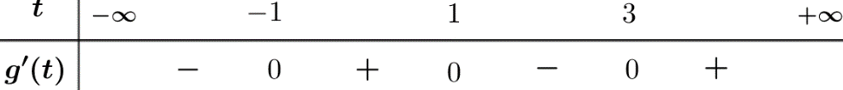

Từ bảng xét dấu ta thấy hàm số $g\left(t\right)$ đồng biến trên khoảng $\left(-1;1\right)$ và $\left(3;+\infty \right)$

Hay $\left[ \begin{align}& -1<t<1 \\  & t>3 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& -1<x-m<1 \\ & x-m>3 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& m-1<x<m+1 \\ & x>m+3 \\ \end{align} \right.$

Để hàm số $g\left(x\right)$ đồng biến trên khoảng $\left(5;6\right)$ thì $\left[ \begin{align}& m-1\le 5<6\le m+1 \\ & m+3\le 5<6 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& 5\le m\le 6 \\  & m\le 2 \\ \end{align} \right.$

Vì $m$ là các số nguyên dương nên $S=\left\{1;2;5;6\right\}$

Vậy tổng tất cả các phần tử của $S$ là: 1+2+5+6=14.

Câu 38. Cho hàm số $y=f\left(x\right)$ có đồ thị nằm trên trục hoành và có đạo hàm trên $\mathbb{R}$, bảng xét dấu của biểu thức ${f}'\left(x\right)$ như bảng dưới đây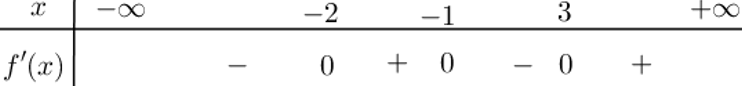

Hàm số $y=g\left(x\right)=\dfrac{f\left({{x}^{2}}-2x\right)}{f\left({{x}^{2}}-2x\right)+1}$ nghịch biến trên khoảng nào dưới đây?

A. $\left(-\infty ;1\right)$.       B. $\left(-2;\dfrac{5}{2}\right)$.       C. $\left(1;\,3\right)$.       D. $\left(2;+\infty \right)$.

Lời giải:

${g}'\left(x\right)=\dfrac{{{\left({{x}^{2}}-2x\right)}^{\prime}}.{f}'\left({{x}^{2}}-2x\right)}{{{\left(f\left({{x}^{2}}-2x\right)+1\right)}^{2}}}=\dfrac{\left(2x-2\right).{f}'\left({{x}^{2}}-2x\right)}{{{\left(f\left({{x}^{2}}-2x\right)+1\right)}^{2}}}$.

${g}'\left( x \right)=0$ $\Leftrightarrow \left[ \begin{align}& 2x-2=0 \\ & {f}'\left( {{x}^{2}}-2x \right)=0 \\\end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& x=1 \\ & {{x}^{2}}-2x=-2 \\ & {{x}^{2}}-2x=-1 \\ & {{x}^{2}}-2x=3 \\ \end{align} \right.$ $\Leftrightarrow \left[ \begin{align}& x=1 \\ & x=-1 \\ & x=3 \\ \end{align} \right.$

Ta có bảng xét dấu của ${g}'\left(x\right)$:

 

Dựa vào bảng xét dấu ta có hàm số $y=g\left(x\right)$ nghịch biến trên các khoảng $\left(-\infty \,;\,-1\right)$ và $\left(1\,;\,3\right)$.

Câu 39. Cho hàm số $f\left(x\right)$ xác định và liên tục trên $\mathbb{R}$ và có đạo hàm ${f}'\left(x\right)$ thỏa mãn ${f}'\left(x\right)=\left(1-x\right)\left(x+2\right)g\left(x\right)+2019$ với $g\left(x\right)<0$, $\forall x\in \mathbb{R}$. Hàm số $y=f\left(1-x\right)+2019x+2020$ nghịch biến trên khoảng nào?

A. $\left(1;\,+\infty \right)$.       B. $\left(0;\,3\right)$.       C. $\left(-\infty ;\,3\right)$.       D. $\left(3;\,+\infty \right)$.

Lời giải:

Đặt $h\left(x\right)=f\left(1-x\right)+2019x+2020$.

Vì hàm số $f\left(x\right)$ xác định trên $\mathbb{R}$ nên hàm số $h(x)$ cũng xác định trên $\mathbb{R}$.

Ta có ${h}'\left(x\right)=-{f}'\left(1-x\right)+2019$.

Do ${h}'\left(x\right)=0$ tại hữu hạn điểm nên để tìm khoảng nghịch biến của hàm số $h\left(x\right)$, ta tìm các giá trị của $x$ sao cho ${h}'\left(x\right)<0$ $\Leftrightarrow  $$-{f}'\left(1-x\right)+2019<0$ $\Leftrightarrow  $ ${f}'\left(1-x\right)-2019>0$

$\Leftrightarrow$ $x.(3-x).g(1-x)$ $\Leftrightarrow$ $x\left(3-x\right)<0$ $\Leftrightarrow$ $\left[\begin{align}&x<0\\ &x>3\end{align}\right.$.

Vậy hàm số $y=f\left(1-x\right)+2019x+2020$ nghịch biến trên các khoảng $\left(-\infty ;0\right)$ và $\left(3;\,+\infty \right)$.

Câu 40. Cho hàm số $f(x)=\dfrac{{{x}^{5}}}{5}-{{x}^{2}}+(m-1)x-4029$. Có bao nhiêu giá trị nguyên của $m$ để hàm số $y=|f(x-1)+2022|$ nghịch biến trên $(-\infty ;2)$?

A. 2005.       B. 2006.       C. 2007.       D. 2008.

Lời giải:

Đặt $h\left(x\right)=f\left(x-1\right)+2022$.

Ta có $y=\left|f\left(x-1\right)+2022\right|$ nghịch biến trên $\left(-\infty ;2\right)$ thì

$\left\{\begin{align}&f\left(x-1\right)+2022\le0\\ &{h}'\left(x\right)\ge0\end{align}\right.\forall x\in \left(-\infty ;2\right)$ $\Leftrightarrow  \left\{\begin{align}&f\left(1\right)+2022\le0\,\,\,\\ &{h}'\left(x-1\right)\ge0\,\end{align}\right.\forall x\in \left(-\infty ;2\right)$ $\Leftrightarrow  \left\{\begin{align}&m\le\dfrac{10044}{5}\,\,\,\left(1\right)\\ &{h}'\left(x-1\right)\ge0\,\,\forall x\in \left(-\infty ;2\right)\,\,(2)\end{align}\right.$ $\Leftrightarrow  \left\{\begin{align}&m\le\dfrac{10044}{5}\,\,\,\left(1\right)\\ &{{\left(x-1\right)}^{4}}-2\left(x-1\right)+m-1\ge0\,\,\forall x\in \left(-\infty ;2\right)\,\,(2)\end{align}\right.$

Đặt $t=x-1,$ $t\in \left(-\infty ;1\right)$, khi đó ta có

$\left(2\right)\Leftrightarrow  {{t}^{4}}-2t+m-1\ge0\,\,\forall \,\,t\in \left(-\infty ;1\right)$

$\Leftrightarrow  -{{t}^{4}}+2t+1\le m\,\,\forall \,\,t\in \left(-\infty ;1\right)$

Đặt $g(t)=-{{t}^{4}}+2t+11$ $\Rightarrow {{g}^{'}}(t)=-4{{t}^{3}}+2$.

Xét ${{g}^{'}}(t)=0\Leftrightarrow  -4{{t}^{3}}+2=0\Leftrightarrow  t=\dfrac{1}{\sqrt[3]{2}}$.

Nên $\Leftrightarrow  f\left(\dfrac{1}{\sqrt[3]{2}}\right)\le m\,\Leftrightarrow  m\ge\dfrac{3}{3\sqrt[3]{2}}+1$

Từ và suy ra $\dfrac{3}{3\sqrt[3]{2}}+1\le m\le\dfrac{10044}{5}$, mà $m\in \mathbb{Z}$ nên có 2007 giá trị $m$ thỏa mãn yêu cầu bài toán.

Nguyễn Quốc Hoàn , 02/3/2023