Đề toán 12 kì 2 trường THPT Nguyễn Gia Thiều năm học 2024-2025

Sáng ngày 15/4/2025 tại trường THPT Nguyễn Gia Thiều – Hà Nội, đã chính thức kiểm tra cuối kì 2 môn toán lớp 12 năm học 2024–2025. Đề kiểm tra chung toàn trường cho gần 700 học sinh, với 02 đề gốc khác nhau được trộn làm 24 mã đề khác nhau để chia về các phòng kiểm tra.

Đề phủ đầy đủ các chủ đề trọng tâm của học kỳ II lớp 12 theo chương trình giáo dục phổ thông 2018, có nhiều bài toán thực tế được đưa vào các câu hỏi trong đề, bao gồm Hình học giải tích trong không gian $Oxyz$ (điểm, vectơ, mặt phẳng, đường thẳng, mặt cầu, khoảng cách, góc, …), Nguyên hàm Tích phân và Ứng dụng của tích phân, và Xác suất (cơ bản, điều kiện, công thức nhân xác suất, xác suất toàn phần, Bayes). Đây cũng là những chủ đề lớn cần ôn tập để thi TN THPT QG 2025. Đề kiểm tra gồm 3 phần trắc nghiệm:

Phần I: Trắc nghiệm khách quan với 4 lựa chọn; kiểm tra kiến thức cơ bản. Độ nhiễu cao ở các phương án chọn góp phần làm tăng độ hấp dẫn của đề kiểm tra.

Phần II: Câu hỏi Đúng/Sai yêu cầu nhiều hơn so với việc áp dụng công thức đơn thuần, đòi hỏi kiểm tra điều kiện cẩn thận, giải thích định nghĩa và công thức chính xác, khả năng diễn giải và phân tích đồ thị, thực hiện các bước tính toán phức tạp trong một ngữ cảnh cụ thể. Câu hỏi có cấu trúc rõ ràng (a, b, c, d), dẫn dắt học sinh qua các bước phân tích khác nhau của cùng một tình huống và qua đó định hướng học sinh tự tìm tòi cách giải quyết vấn đề đặt ra. Nhiều câu hỏi rất hay có sự phân hóa tốt, sự phân hóa còn thể hiện ngay chính trong cùng một câu hỏi, những bài toán thực tế có nhiều thử thách cao cũng góp phần kích thích cho học sinh.

Phần III: Trả lời ngắn yêu cầu học sinh tự trình bày, tự giải quyết hoàn chỉnh các bài toán từ đơn giản đến phức tạp, phần này có sự phân hóa rất cao với các câu hỏi đa dạng, ứng dụng thực tế vào nhiều lĩnh vực khác nhau của cuộc sống và có tính thử thách cao. Có tình huống thực tế thú vị và gần gũi với học sinh, giúp học sinh thấy được ứng dụng của xác suất trong đời sống có ý nghĩa hơn. Mô phỏng được các bài toán về tăng trưởng, tích lũy trong kinh tế, tài chính, kết nối toán học với thực tiễn. Có những câu hỏi đơn giản nhưng được đặt trong bối cảnh không gian thực làm tăng hứng thú khi làm toán. Phần II và phần III, đánh giá tư duy rất sâu, chi tiết và đầy đủ.

Nhiều câu hỏi được đặt trong bối cảnh thực tế rất hay và thực sự phù hợp thực tế chứ không hề phi thực tế, góp phần làm tăng tính hấp dẫn cho môn toán (như: xét nghiệm y tế, phủ sóng điện thoại, khảo sát, đường bay, thị phần, di chuyển, muộn học . . .). Học sinh không chỉ làm bài kiểm tra đánh giá thông thường mà còn được tập dượt bước đầu vận dụng toán học phổ thông vào các lĩnh vực khác nhau của cuộc sống.

Đề kiểm tra không lỗi không sai sót, đảm bảo tính khoa học và chính xác, đề kiểm tra có giá trị sư phạm cao, không xuất hiện những câu hỏi ngoài chương trình. Đề trình bày rõ ràng, đẹp và bố cục hợp lý, câu hỏi cũng rõ ràng rõ nghĩa không gây hiểu nhầm khi đọc đề. Các dạng bài tập đa dạng, từ cơ bản đến nâng cao, từ toán học thuần túy đến toán ứng dụng, đánh giá được nhiều năng lực quan trọng của học sinh và có độ phân hóa cao. Có thể nói đây là một đề kiểm tra có chất lượng cao nhất, rất hay và tốt phù hợp với chương trình hiện hành. Đánh giá khách quan được nhiều năng lực cốt lõi của học sinh theo yêu cầu của chương trình GDPT 2018.

Xin cảm ơn thầy giáo Nguyễn Quốc Hoàn đã ra đề kiểm tra rất tốt; giúp Nhà trường, Giáo viên và Học sinh có định hướng rõ ràng và đúng cho việc dạy và học hiện nay. Ngoài ra, đề cương và ma trận đề đã công khai trước đó của thầy ra cũng phù hợp với nội dung đề kiểm tra này, tạo thành một bộ thống nhất đồng bộ chặt chẽ: chương trình hiện hành + đề cương ôn tập + ma trận đề toán + đề kt đánh giá.

Sau đây là nội dung 2 mã đề và đáp án kèm theo:

ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2024-2025 MÔN TOÁN LỚP 12

Đề trộn thứ nhất

Phần I.  Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu học sinh chỉ chọn một phương án.

Câu 1.  Cho hàm số $f\left( x \right)\,\,=\,\,{{e}^{2x}}$. Khi đó

A. $\int{f\left( x \right)\text{d}x\,\,=\,\,{{e}^{2x}}+C}$.

B. $\int{f\left( x \right)\text{d}x\,\,=\,\,2{{e}^{2x}}+C}$.

C. $\int{f\left( x \right)\text{d}x\,\,=\,\,\dfrac{1}{2}{{e}^{2x}}+C}$.  

D. $\int{f\left( x \right)\text{d}x\,\,=\,\,2{{e}^{x}}+C}$.

Đáp án:  C.

Câu 2.  Cho hai biến cố ${A}$ và ${B.}$ Xác suất của biến cố ${A}$ với điều kiện biến cố ${B}$ đã xảy ra được gọi là xác suất của ${A}$ với điều kiện $B$, kí hiệu là $\text{P}(A\mid B)$. Chọn khẳng định đúng trong các khẳng định sau đây

A. Nếu ${P(A)>0}$ thì $\text{P}(A\mid B)=\dfrac{\text{P}(A\cap B)}{\text{P}(A)}$.

B. Nếu ${P(B)>0}$ thì $\text{P}(A\mid B)=\dfrac{\text{P}(A\cap B)}{\text{P}(B)}$.

C. Nếu ${P(B)>0}$ thì $\text{P}(A\mid B)=\dfrac{\text{P}(A\cap B)}{\text{P}(A)}$.        

D. Nếu $\text{P}(A)>0$ thì $\text{P}(A\mid B)=\dfrac{\text{P}(A\cap B)}{\text{P}(B)}$.

Đáp án:  B.

Câu 3.  Cho hai biến cố $M,~~N$ với $0\,\,<\,\,\text{P}(N)\,\,<\,\,1$. Chọn khẳng định đúng trong các khẳng định sau đây

A. ${\text{P}(M)=\text{P}\left( \overline{N} \right).\text{P}\left( M\mid N \right)+\text{P}(N).\text{P}\left( M\mid \overline{N} \right)}$.

B. ${\text{P}(M)=\text{P}(N).\text{P}\left( M\mid N \right)-\text{P}(\overline{N}).\text{P}\left( M\mid \overline{N} \right)}$.

C. ${\text{P}(M)=\text{P}(\overline{N}).\text{P}\left( M\mid \overline{N} \right)-\text{P}(N).\text{P}\left( M\mid N \right)}$.            

D. ${\text{P}(M)=\text{P}(N).\text{P}\left( M\mid N \right)+\text{P}(\overline{N}).\text{P}\left( M\mid \overline{N} \right)}$.

Đáp án:  D.

Câu 4.  Cho hai biến cố ${A}$, ${B}$ sao cho $\text{P}(A)=0,6$; $\text{P}(B)=0,5$; $\text{P}(A\mid B)=0,2$. Khi đó $\mathrm{P}(B \mid A)$ bằng

A. $\dfrac{6}{25}$.

B. $\dfrac{3}{25}$.                                  

C. $\dfrac{1}{6}$.                                   

D. $\dfrac{1}{3}$.

Đáp án:  C.

Câu 5. Cho hai biến cố $A,\,\,B$ với $P\left( B \right)=0,6$; $\text{P}\left( A\left| B \right. \right)=0,5$. Khi đó $P\left( AB \right)$ bằng

A. $\dfrac{3}{10}$.   

B. $\dfrac{5}{6}$.                                       

C. $\dfrac{1}{2}$.                                       

D. $\dfrac{3}{5}$.

Đáp án:  A.

Câu 6. Trong không gian với hệ tọa độ ${Oxyz}$, mặt phẳng $2x-4y+8z-1\,\,=\,\,0$ có một vectơ pháp tuyến là

A. $\vec{n}=\left( 1\,\,;\,\,2\,\,;\,\,4 \right)$.   

B. $\vec{n}=\left( 1\,\,;\,\,-2\,\,;\,\,4 \right)$.           

C. $\vec{n}=\left( 2\,\,;\,\,-4\,\,;\,\,4 \right)$.         

D. $\vec{n}=\left( 2\,\,;\,\,-4\,\,;\,\,1 \right)$.

Đáp án:  B.

Câu 7. Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $M\left( 1\,\,\,;\,\,\,0\,\,;\,\,-1 \right)$ và $N\left( 3\,\,;\,\,2\,\,;\,\,-9 \right)$. Đường thẳng $MN$ có phương trình là

A. $\dfrac{x+1}{1}=\dfrac{y}{1}=\dfrac{z-1}{-4}$.

B. $\dfrac{x-1}{1}=\dfrac{y}{1}=\dfrac{z+1}{4}$.             

C. $\dfrac{x+1}{1}=\dfrac{y}{1}=\dfrac{z-1}{4}$.           

D. $\dfrac{x-1}{1}=\dfrac{y}{1}=\dfrac{z+1}{-4}$.

Đáp án:  D.

Câu 8. Trong không gian với hệ tọa độ $Oxyz$, mặt cầu tâm $I(1\,\,;\,\,-4\,\,;\,\,1)$, bán kính $R=4$ có phương trình

A. ${{{\left( x\,\,-\,\,1 \right)}^{2}}\,\,+\,\,{{\left( y\,\,+\,\,4 \right)}^{2}}\,\,+\,\,{{\left( z\,\,-\,\,1 \right)}^{2}}\,\,=\,\,16}$.

B. ${{{\left( x\,\,-\,\,1 \right)}^{2}}\,\,+\,\,{{\left( y\,\,+\,\,4 \right)}^{2}}\,\,+\,\,{{\left( z\,\,-\,\,1 \right)}^{2}}\,\,=\,\,2}$.

C. ${{{\left( x\,\,+\,\,1 \right)}^{2}}\,\,+\,\,{{\left( y\,\,-\,\,4 \right)}^{2}}\,\,+\,\,{{\left( z\,\,+\,\,1 \right)}^{2}}\,\,=\,\,16}$.                          

D. ${{{\left( x\,\,-\,\,1 \right)}^{2}}\,\,+\,\,{{\left( y\,\,+\,\,4 \right)}^{2}}\,\,+\,\,{{\left( z\,\,-\,\,1 \right)}^{2}}\,\,=\,\,4}$.

Đáp án:  A.

Câu 9. Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $\left( P \right):\,\,x+y+4z-1=0$ và $\left( Q \right):x-z=0$. Góc giữa hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ bằng

A. ${{0}^{0}}$.

B. ${{30}^{0}}$.                                    

C. ${{45}^{0}}$.                                

D. ${{60}^{0}}$.

Đáp án:  D.

Câu 10. Cho bảng dữ liệu sau về kết quả xét nghiệm một loại bệnh:

	Dương tính	Âm tính
Bệnh	120	30
Không bệnh	40	970

Nếu một người có kết quả xét nghiệm dương tính, xác suất người đó thực sự mắc bệnh là

A. 3%.   

B. 11%.                                  

C. 75%.                                 

D. 90%.

Đáp án:  C.

Câu 11. Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số ${y=f\left( x \right)}$, trục hoành, trục tung và đường thẳng ${x=a}$, ${a>0}$ (phần tô đậm trong hình vẽ) được tính theo công thức

A. $S=\int\limits_{0}^{c}{f(x)\,\text{d}x}-\int\limits_{c}^{a}{f(x)\,\text{d}x}$.

B. $S=-\int\limits_{0}^{a}{f(x)\,\text{d}x}$.

C. $S=-\int\limits_{0}^{c}{f(x)\,\text{d}x}+\int\limits_{c}^{a}{f(x)\,\text{d}x}$.  

D. $S=\int\limits_{0}^{c}{f(x)\,\text{d}x}+\int\limits_{c}^{a}{f(x)\,\text{d}x}$.

Đáp án:  A.

Câu 12. Khi đặt hệ tọa độ ${Oxyz}$ vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy rằng một không gian phủ sóng điện thoại có dạng một hình cầu ${(S)}$ (tập hợp những điểm nằm trong và nằm trên mặt cầu tương ứng). Biết mặt cầu ${(S)}$ có phương trình ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}-4x-2y-8z+5=0$. Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là

A. 10 kilômét.

B. 8 kilômét.                     

C. 5 kilômét.                       

D. 4 kilômét.

Đáp án:  B.

 

Phần II.  Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số $f(x)\,\,=\,\,{{x}^{3}}-3{{x}^{2}}+2x$ có đồ thị như hình bên.

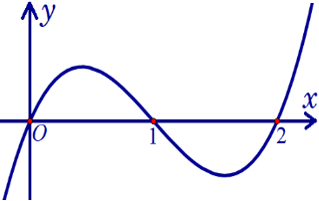a) $\int\limits_{0}^{1}{f'(x)\,\text{d}x\,\,=\,\,0}$.

b)  Gọi $F(x)$ là một nguyên hàm của hàm số $f(x)$, khi đó $F(x)\,\,=\,\,\int{f'(x)\,\text{d}x}$.  

c)  Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, trục hoành và hai đường thẳng $x=0$, $x=2$ là $\int\limits_{0}^{2}{f(x)\,\text{d}x}$.  

d)  Gọi $\left( D \right)$ là hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, trục hoành, trục tung và đường thẳng $x=1$. Thể tích khối tròn xoay được tạo thành khi quay $\left( D \right)$ quanh trục hoành được tính theo công thức $\pi \int\limits_{0}^{1}{{{f}^{2}}(x)\,\text{d}x}$.

Đáp án:  Đ S S Đ.

Câu 2. Trong cuộc khảo sát ngẫu nhiên 600 học sinh về việc “thích học” hay “không thích học” môn toán. Kết quả thống kê như sau: có 400 học sinh trả lời "thích học" và 200 học sinh trả lời "không thích học". Thực tế cho thấy tỉ lệ học sinh “giỏi toán” tương ứng với những cách trả lời "thích học" và "không thích học" lần lượt là 70% và 10%.

Gọi $T$ là biến cố "Học sinh được phỏng vấn trả lời thích học môn toán".

Gọi $G$ là biến cố "Học sinh được phỏng vấn giỏi toán".

a) Xác suất $\text{P}\left( T \right)\,\,=\,\,\dfrac{2}{3}$ và $\text{P}\left( \overline{T} \right)\,\,=\,\,\dfrac{1}{3}$.

b)  Xác suất có điều kiện $\text{P}\left( G\mid T \right)=0,3$, $\text{P}\left( G\mid \overline{T} \right)=0,9$.    

c)  Xác suất $\text{P}(G)=0,5$.  

d)  Trong số những người được phỏng vấn giỏi toán có 80% người đã trả lời thích học môn toán khi được phỏng vấn (kết quả tính theo phần trăm được làm tròn đến hàng đơn vị).

Đáp án:  Đ S Đ S.

Câu 3.  Gọi hàm số $F\left( x \right)=\dfrac{2{{x}^{2}}-1}{x}$ là một nguyên hàm của hàm số $f(x)$, với $x\,\,\ne \,\,0$.

a) $f\left( x \right)\,\,=\,\,2-\dfrac{1}{{{x}^{2}}}$.  

b)  $\int{f(x)\,\text{d}x}\,\,=\,\,\dfrac{2{{x}^{2}}-1}{x}\,\,+\,\,C$.   

c)  $\int{F(x)\,\text{d}x}\,\,=\,\,f(x)\,\,+\,\,C$.         

d) $\int{F(x)\,\text{d}x}\,\,=\,\,{{x}^{2}}\,\,-\,\,\ln \left| x \right|\,\,+\,\,C$.

Đáp án:  S Đ S Đ.

Câu 4. Trong không gian với hệ tọa độ $Oxyz$ (đơn vị trên các trục là kilômét), mặt đất được coi là mặt phẳng $(Oxy)$ có phương trình $z=0$. Tại gần sân bay có một máy bay dân dụng đang thực hiện quá trình hạ cánh, bắt đầu từ vị trí điểm $A\left( 38\,\,;\,\,-16\,\,;\,\,6 \right)$ và bay thẳng đến vị trí điểm $B\left( -2\,\,;\,\,4\,\,;\,\,1 \right)$ gần đường băng. Máy bay duy trì tốc độ không đổi là 270$km\text{/}h$ trong suốt quá trình hạ cánh.

a) Phương trình tham số của đường thẳng $d$ biểu diễn đường bay của máy bay từ $A$ đến $B$ là: $\left\{ \begin{align} & x\,\,=\,\,38\,\,-\,\,8t \\  & y\,\,=\,\,-16\,\,+\,\,4t \\  & z\,\,=\,\,6\,\,-\,\,t \\ \end{align} \right.$ ($t$ là tham số hình học).    

b)  Quá trình hạ cánh máy bay đi qua vị trí điểm $C\left( 46\,\,;\,\,-20\,\,;\,\,7 \right)$.    

c)  Quy định về an toàn bay yêu cầu góc hạ cánh (góc giữa đường bay và mặt đất) không được lớn hơn ${{5}^{0}}$. Đường bay này đã tuân thủ đúng quy định an toàn.   

d)  Sau 5 phút kể từ khi bắt đầu hạ cánh máy bay ở vị trí điểm ${M\left( 18\,\,;\,\,-6\,\,;\,\,\dfrac{7}{2} \right)}$.

Đáp án:  Đ S S Đ.

 

Phần III.  Học sinh trả lời từ câu 1 đến câu 6.

Câu 1. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y\,\,=\,\,\cos x$, trục hoành, trục tung và đường thẳng $x\,\,=\,\,\dfrac{\pi }{6}$ ?

Đáp án:  0,5.

Câu 2. Gieo con xúc xắc cân đối và đồng chất một lần. Gọi ${A}$ là biến cố xuất hiện mặt 1 chấm, $B$ là biến cố xuất hiện mặt lẻ chấm. Tính xác suất có điều kiện $\text{P}\left( A\left| B \right. \right)$? (kết quả làm tròn đến hàng phần trăm).

Đáp án:  0,33.

Câu 3. Một người điều khiển Flycam đang đứng tại một điểm được xem là gốc tọa độ $O(0\,\,;\,\,0\,\,;\,\,0)$ trong không gian. Các trục tọa độ được quy ước như sau: Trục ${Ox}$ theo hướng Đông; trục ${Oy}$ theo hướng Bắc; trục ${Oz}$ theo hướng thẳng đứng lên trên; đơn vị mỗi trục là mét. Tại một thời điểm, Flycam ở vị trí ${A}$ có tọa độ $(1;-8;4)$. Khoảng cách (đường chim bay) từ người điều khiển đến Flycam tại vị trí ${A}$ là mấy mét ?

Đáp án:  9.

Câu 4. Bạn An đi học mỗi ngày bằng một trong hai phương tiện: xe buýt hoặc xe đạp. Vì vội, An chọn ngẫu nhiên một trong hai phương tiện này với xác suất như nhau (tức là 50% đi xe buýt, 50% đi xe đạp). Nếu An đi xe buýt thì xác suất bị muộn học là 6%; nếu An đi xe đạp thì xác suất bị muộn học là 4%. Hỏi vào một ngày bất kỳ, xác suất An bị muộn học là bao nhiêu ?

Đáp án:  0,05.

Câu 5. Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d:\,\,\dfrac{x-1}{2}\,\,=\,\,\dfrac{y-1}{-1}\,\,=\,\,\dfrac{z-4}{2}$ và mặt cầu $(S):\,\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}=9$. Gọi $(P)$ là mặt phẳng có phương trình dạng: $ax+by+cz+9=0$. Biết rằng $(P)$ chứa $d$ và $(P)$ tiếp xúc với $(S)$. Tính giá trị biểu thức $a+b+c$ ?

Đáp án:  –3.

Câu 6. Hai công ty, công ty A và công ty B, cùng ra mắt sản phẩm cạnh tranh thị trường mới vào cùng thời điểm. Thị phần được đo bằng số lượng khách hàng lũy kế.

Công ty A: Bắt đầu với 0 khách hàng. Trong giai đoạn đầu, chiến dịch marketing hiệu quả giúp tốc độ thu hút khách hàng mới của họ tăng dần theo thời gian, được mô tả bởi hàm $f(t)=2t+7$ (nghìn khách hàng/tháng), với ${t}$ là số tháng kể từ khi ra mắt.

Công ty B: Nhờ có uy tín từ trước, họ bắt đầu với 10 nghìn khách hàng đặt trước sản phẩm. Sau đó, họ duy trì một tốc độ thu hút khách hàng mới ổn định là 10 nghìn khách hàng/tháng.

Hỏi sau khoảng bao nhiêu tháng kể từ khi ra mắt, tổng số lượng khách hàng lũy kế của công ty A bằng tổng số lượng khách hàng lũy kế của công ty B (tính cả 10 nghìn khách hàng ban đầu) ?

Đáp án:  5.

 

Đề trộn thứ hai

Phần I.  Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu học sinh chỉ chọn một phương án.

Câu 1.  Cho hàm số $f\left( x \right)\,\,=\,\,{{e}^{3x}}$. Khi đó

A. $\int{f\left( x \right)\text{d}x\,\,=\,\,3{{e}^{3x}}+C}$.

B. $\int{f\left( x \right)\text{d}x\,\,=\,\,\dfrac{1}{3}{{e}^{3x}}+C}$.

C. $\int{f\left( x \right)\text{d}x\,\,=\,\,{{e}^{3x}}+C}$.  

D. $\int{f\left( x \right)\text{d}x\,\,=\,\,3{{e}^{x}}+C}$.

Đáp án:  B.

Câu 2.  Cho hai biến cố $M$ và $N$. Xác suất của biến cố $M$ với điều kiện biến cố $N$ đã xảy ra được gọi là xác suất của $M$ với điều kiện $N$, kí hiệu là $\text{P}(M\mid N)$. Chọn khẳng định đúng từ các khẳng định sau

A. Nếu $\text{P}(N)>0$ thì $\text{P}(M\mid N)=\dfrac{\text{P}(M\cap N)}{\text{P}(M)}$.

B. Nếu $\text{P}(M)>0$ thì $\text{P}(M\mid N)=\dfrac{\text{P}(M\cap N)}{\text{P}(N)}$.  

C. Nếu $\text{P}(M)>0$ thì $\text{P}(M\mid N)=\dfrac{\text{P}(M\cap N)}{\text{P}(M)}$.

D. Nếu $\text{P}(N)>0$ thì $\text{P}(M\mid N)=\dfrac{\text{P}(M\cap N)}{\text{P}(N)}$.

Đáp án:  D.

Câu 3.  Cho hai biến cố $A,~~B$ với $0<\text{P}(B)<1$. Chọn khẳng định đúng từ các khẳng định sau

A. $\text{P}(A)=\text{P}(\bar{B}).\text{P}(A\mid \bar{B})-\text{P}(B).\text{P}(A\mid B)$.

B. $\text{P}(A)=\text{P}(B).\text{P}(A\mid B)+\text{P}(\bar{B}).\text{P}(A\mid \bar{B})$.  

C. $\text{P}(A)=\text{P}(\bar{B}).\text{P}(A\mid B)+\text{P}(B).\text{P}(A\mid \bar{B})$.                             

D. $\text{P}(A)=\text{P}(B).\text{P}(A\mid B)-\text{P}(\bar{B}).\text{P}(A\mid \bar{B})$.

Đáp án:  B.

Câu 4.  Cho hai biến cố $A$, $B$ sao cho $\text{P}(A)=0,6$; $\text{P}(B)=0,5$; $\text{P}\left( B\left| A \right. \right)=0,2$. Khi đó $\text{P}\left( A\mid B \right)$ bằng

A. $\dfrac{6}{25}$.

B. $\dfrac{1}{6}$.

C. $\dfrac{3}{25}$.                                

D. $\dfrac{1}{3}$.

Đáp án:  A.

Câu 5. Cho hai biến cố $A,\,\,B$ với $\text{P}\left( A \right)=0,8$; $\text{P}\left( B\left| A \right. \right)=0,5$. Khi đó $\text{P}\left( AB \right)$ bằng

A. $\dfrac{2}{5}$.

B. $\dfrac{5}{8}$.                                   

C. $\dfrac{1}{2}$.                            

D. $\dfrac{4}{5}$.                       

Đáp án:  A.

Câu 6. Trong không gian với hệ tọa độ $Oxyz$, cho điểm $M\left( -1\,\,;\,\,1\,\,;\,\,0 \right)$ và mặt phẳng ${\left( P \right):\,\,8x\,\,-\,\,2y\,\,+\,\,2z\,\,-\,\,1\,\,=\,\,0}$.  Đường thẳng đi qua $M$ và vuông góc với $\left( P \right)$ có phương trình là

A. $\dfrac{x-1}{4}=\dfrac{y+1}{-1}=\dfrac{z}{1}$.

B. $\dfrac{x+1}{4}=\dfrac{y-1}{-2}=\dfrac{z}{2}$.

C. $\dfrac{x+1}{4}=\dfrac{y-1}{-1}=\dfrac{z}{1}$.          

D. $\dfrac{x+1}{4}=\dfrac{y-1}{1}=\dfrac{z}{1}$.

Đáp án:  C.

Câu 7. Cho bảng dữ liệu sau về kết quả xét nghiệm một loại bệnh:

	Dương tính	Âm tính
Bệnh	120	30
Không bệnh	40	970

Nếu một người có kết quả xét nghiệm âm tính, xác suất người đó thực sự mắc bệnh là

A. 3%.

B. 11%.                                  

C. 75%.                             

D. 90%.

Đáp án:  A.

Câu 8. Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số ${y=f\left( x \right)}$, trục hoành, trục tung và đường thẳng ${x=a}$, ${a>0}$  (phần tô đậm trong hình vẽ) được tính theo công thức

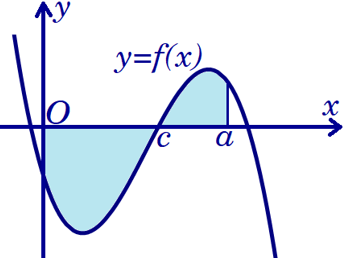A. $S=\int\limits_{0}^{c}{f(x)\,\text{d}x}+\int\limits_{c}^{a}{f(x)\,\text{d}x}$.

B. $S=\int\limits_{0}^{c}{f(x)\,\text{d}x}-\int\limits_{c}^{a}{f(x)\,\text{d}x}$.

C. $S=-\int\limits_{0}^{a}{f(x)\,\text{d}x}$.                            

D. $S=-\int\limits_{0}^{c}{f(x)\,\text{d}x}+\int\limits_{c}^{a}{f(x)\,\text{d}x}$.

Đáp án:  D.

Câu 9. Trong không gian với hệ tọa độ $Oxyz$, mặt cầu ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-2y-8z+2=0$ có toạ độ tâm là

A. $I\left( 2;2;8 \right)$.

B. $I\left( -1;-1;-4 \right)$.

C. $I\left( -2;-2;-8 \right)$.                

D. $I\left( 1;1;4 \right)$.

Đáp án:  D.

Câu 10. Trong không gian với hệ tọa độ ${Oxyz}$, mặt phẳng $2x-4y-8z-1\,\,=\,\,0$ có một vectơ pháp tuyến là

A. $\vec{n}=\left( 1\,\,;\,\,-2\,\,;\,\,4 \right)$.

B. $\vec{n}=\left( 1\,\,;\,\,2\,\,;\,\,4 \right)$.       

C. $\vec{n}=\left( -1\,\,;\,\,2\,\,;\,\,4 \right)$.         

D. $\vec{n}=\left( 2\,\,;\,\,-4\,\,;\,\,4 \right)$.

Đáp án:  C.

Câu 11. Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d:\left\{ \begin{align} & x=-2{{t}_{1}} \\  & y=-2{{t}_{1}} \\  & z=4+{{t}_{1}} \\ \end{align} \right.$ và $\Delta :\left\{ \begin{align}  & x={{t}_{2}} \\  & y=7 \\  & z=-{{t}_{2}} \\ \end{align} \right.$. Góc giữa hai đường thẳng $d$ và $\Delta $ bằng   

A. ${{30}^{0}}$.

B. ${{45}^{0}}$.

C. ${{60}^{0}}$.              

D. ${{90}^{0}}$.

Đáp án:  B.

Câu 12. Khi đặt hệ tọa độ $Oxyz$ vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy rằng một không gian phủ sóng điện thoại có dạng một hình cầu ${(S)}$ (tập hợp những điểm nằm trong và nằm trên mặt cầu tương ứng). Biết mặt cầu ${(S)}$ có phương trình ${{x}^{2}}+{{y}^{2}}+{{z}^{2}}-4x-2y-8z+12=0$. Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là

A. 3 kilômét.

B. 5 kilômét.                             

C. 6 kilômét.                       

D. 10 kilômét.

Đáp án:  C.

 

Phần II.  Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.

Câu 1.  Gọi hàm số $F\left( x \right)=\dfrac{1\,\,-\,\,{{e}^{x}}}{{{e}^{x}}}$ là một nguyên hàm của hàm số $f(x)$.

a) $f\left( x \right)\,\,=\,\,{{e}^{-x}}$.

b)  $\int{f(x)\,\text{d}x}\,\,=\,\,\dfrac{1\,\,-\,\,{{e}^{x}}}{{{e}^{x}}}\,\,+\,\,C$.    

c)  $\int{F(x)\,\text{d}x}\,\,=\,\,f(x)\,\,+\,\,C$.                 

d) $\int{F(x)\,\text{d}x}\,\,=\,\,-x\,\,-\,\,{{e}^{-x}}\,\,+\,\,C$.

Đáp án:  S Đ S Đ.

Câu 2. Cho hàm số $f(x)\,\,=\,\,-{{x}^{3}}+3{{x}^{2}}-2x$ có đồ thị như hình bên.

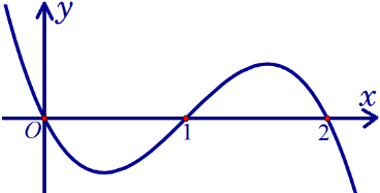a) $\int\limits_{0}^{1}{f'(x)\,\text{d}x\,\,=\,\,0}$.

b)  Gọi $F(x)$ là một nguyên hàm của hàm số $f(x)$, khi đó $F(x)\,\,=\,\,\int{f'(x)\,\text{d}x}$.  

c)  Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, trục hoành và hai đường thẳng $x=0$, $x=2$ là $\int\limits_{0}^{2}{f(x)\,\text{d}x}$.  

d)  Gọi ${D}$ là hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, trục hoành và hai đường thẳng $x=1$, $x=2$. Thể tích khối tròn xoay được tạo thành khi quay ${D}$ quanh trục hoành được tính theo công thức $\pi \int\limits_{1}^{2}{{{f}^{2}}(x)\,\text{d}x}$.

Đáp án:  Đ S S Đ.

Câu 3. Một ngân hàng phân loại các đơn xin vay vốn thành hai nhóm: "Rủi ro cao" và "Rủi ro thấp". Dựa trên dữ liệu lịch sử, ngân hàng ước tính rằng 30% tổng số đơn xin vay thuộc nhóm rủi ro cao. Thực tế cho thấy tỷ lệ các khoản vay bị vỡ nợ (không trả được) trong nhóm rủi ro cao là 15%, trong khi tỷ lệ này ở nhóm rủi ro thấp chỉ là 2%. Ngân hàng chọn ngẫu nhiên một hồ sơ vay vốn đã được duyệt.

Gọi $C$ là biến cố "Hồ sơ vay vốn thuộc nhóm rủi ro cao".

Gọi $V$ là biến cố " Khoản vay bị vỡ nợ".

a) Xác suất $\text{P}\left( C \right)\,\,=\,\,\dfrac{3}{10}$ và $\text{P}\left( \overline{C} \right)\,\,=\,\,\dfrac{7}{10}$.

b)  Xác suất có điều kiện $\text{P}\left( V\mid C \right)=0,85$, $\text{P}\left( V\mid \overline{C} \right)=0,98$.  

c)  Xác suất một khoản vay được chọn ngẫu nhiên bị vỡ nợ là $\text{P}(V)=0,5$.  

d)  Trong số những khoản vay bị vỡ nợ, có khoảng 76% khoản vay đến từ nhóm khách hàng rủi ro cao (kết quả tính theo phần trăm được làm tròn đến hàng đơn vị).

Đáp án:  Đ S S Đ.

Câu 4. Trong không gian với hệ tọa độ $Oxyz$ (đơn vị trên các trục là kilômét), mặt đất được coi là mặt phẳng $(Oxy)$ có phương trình $z=0$. Tại gần sân bay có một máy bay dân dụng đang thực hiện quá trình hạ cánh, bắt đầu từ vị trí điểm $A\left( 37\,\,;\,\,-18\,\,;\,\,\dfrac{31}{6} \right)$ và bay thẳng đến vị trí điểm $B\left( -3\,\,;\,\,2\,\,;\,\,\dfrac{1}{6} \right)$ gần đường băng. Máy bay duy trì tốc độ không đổi là 270$km\text{/}h$ trong suốt quá trình hạ cánh.

a) Phương trình tham số của đường thẳng $d$ biểu diễn đường bay của máy bay từ $A$ đến $B$ là: $\left\{ \begin{align} & x\,\,=\,\,37\,\,-\,\,8t \\  & y\,\,=\,\,-18\,\,+\,\,4t \\  & z\,\,=\,\,\dfrac{31}{6}\,\,-\,\,t \\ \end{align} \right.$ ($t$ là tham số hình học).  

b)  Quá trình hạ cánh máy bay đi qua vị trí điểm $C\left( 45\,\,;\,\,-22\,\,;\,\,\dfrac{37}{6} \right)$.  

c)  Quy định về an toàn bay yêu cầu góc hạ cánh (góc giữa đường bay và mặt đất) không được lớn hơn ${{5}^{0}}$. Đường bay này đã tuân thủ đúng quy định an toàn.  

d)  Sau 5 phút kể từ khi bắt đầu hạ cánh máy bay ở vị trí điểm ${M\left( 17\,\,;\,\,-8\,\,;\,\,\dfrac{8}{3} \right)}$.

Đáp án:  Đ S S Đ.

Phần III.  Học sinh trả lời từ câu 1 đến câu 6.

Câu 1. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y\,\,=\,\,\sin x$, trục hoành, trục tung và đường thẳng $x\,\,=\,\,\dfrac{\pi }{3}$ ?

Đáp án:  0,5.

Câu 2. Gieo con xúc xắc cân đối và đồng chất một lần. Gọi ${A}$ là biến cố xuất hiện mặt 4 chấm, $B$ là biến cố xuất hiện mặt chẵn chấm. Tính xác suất có điều kiện $\text{P}\left( A\left| B \right. \right)$? (kết quả làm tròn đến hàng phần trăm).

Đáp án:  0,33.

Câu 3. Một người điều khiển Flycam đang đứng tại một điểm được xem là gốc tọa độ $O(0\,\,;\,\,0\,\,;\,\,0)$ trong không gian. Các trục tọa độ được quy ước như sau: Trục ${Ox}$ theo hướng Đông; trục ${Oy}$ theo hướng Bắc; trục ${Oz}$ theo hướng thẳng đứng lên trên; đơn vị mỗi trục là mét. Tại một thời điểm, Flycam ở vị trí ${A}$ có tọa độ $(-8;1;4)$. Khoảng cách (đường chim bay) từ người điều khiển đến Flycam tại vị trí ${A}$ là mấy mét ?

Đáp án:  9.

Câu 4. Bạn An đi học mỗi ngày bằng một trong hai phương tiện: xe buýt hoặc xe đạp. Vì vội, An chọn ngẫu nhiên một trong hai phương tiện này với xác suất như nhau (tức là 50% đi xe buýt, 50% đi xe đạp). Nếu An đi xe buýt thì xác suất bị muộn học là 4%; nếu An đi xe đạp thì xác suất bị muộn học là 2%. Hỏi vào một ngày bất kỳ, xác suất An bị muộn học là bao nhiêu ?

Đáp án:  0,03.

Câu 5. Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d:\,\,\dfrac{x-1}{2}\,\,=\,\,\dfrac{y-1}{-1}\,\,=\,\,\dfrac{z-4}{2}$ và mặt cầu $(S):\,\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}=9$. Gọi $(P)$ là mặt phẳng có phương trình dạng: $x+by+cz+d=0$. Biết rằng $(P)$ chứa $d$ và $(P)$ tiếp xúc với $(S)$. Tính giá trị biểu thức $b+c+d$ ?

Đáp án:  5.

Câu 6. Hai công ty, công ty A và công ty B, cùng triển khai các dự án tiết kiệm chi phí và bắt đầu ghi nhận khoản tiết kiệm được cùng một thời điểm.

Công ty A: Bắt đầu với khoản tiết kiệm bằng 0. Tại thời điểm $t$ (tính bằng tháng), tốc độ tiết kiệm chi phí của công ty A là $f(t)=2t+4$ (triệu đồng/tháng).

Công ty B: Bắt đầu dự án khi đã có sẵn 20 triệu đồng tiết kiệm được từ các hoạt động sơ bộ trước đó. Công ty B duy trì một tốc độ tiết kiệm chi phí ổn định là 5 triệu đồng/tháng.

Hỏi sau khoảng bao nhiêu tháng kể từ khi bắt đầu ghi nhận, tổng số tiền tiết kiệm lũy kế của công ty A bằng tổng số tiền tiết kiệm lũy kế của công ty B (tính cả 20 triệu đồng ban đầu) ?

Đáp án:  5.

Giáo viên ra đề: Nguyễn Quốc Hoàn.

 

Ấn đây xem và tải file Word Đề cương, ma trận đề toán cuối kì 2 năm học 2024-2025 trường THPT Nguyễn Gia Thiều.

 

Ấn đây để tải file Word CK2, GK2, CK1 và GK1: các mã đề kiểm tra chính thức, ma trận và đề cương của trường THPT Nguyễn Gia Thiều năm học 2024 – 2025.

 

Trung tâm phát triển năng lực bồi dưỡng kiến thức văn hoá Ánh Dương, 38A ngõ 4 đường Lý Sơn, Hà Nội.  ĐT 034 76 77777

 

Thầy cô, Học sinh tải về nếu hỏi mật khẩu thì nhập một trong các mk sau để mở file (NÊN copy và chú ý không dấu cách và không thừa khoảng trắng hay kí tự bất kì):    hs.edu.vn           https://hs.edu.vn/           https://edu365.edu.vn/           https://edu365.edu.vn           edu365.edu.vn           edu365free           freeedu365           edu365.edu.vnfree           edu365 hoc moi luc moi noi

 

(Nếu file quá nhiều lượt tải về trong ngày, xin bấm vào đây xem hướng dẫn để tải ngay)

 

Chúng tôi luôn mong nhận được sự đồng hành, góp ý và chia sẻ của thầy cô giáo và học sinh.

Xin gửi về địa chỉ:

Nhà giáo:    Nguyễn Quốc Hoàn

Mobi, Zalo:    0913 661 886

Tel:    025 99 999 888 ,    024 666 07 999 ,    028 99 99 99 77

Giờ làm việc:    08h11 - 18h36 hàng ngày; trừ các ngày lễ và ngày thứ bẩy, chủ nhật.

Ấn đây để tải File này