Tích phân đề 1 ôn thi tốt nghiệp thpt 2025

TÍCH PHÂN Đề 1 Năm học 2024-2025.  Ôn thi TN THPT môn Toán

Phần 1.  Mỗi câu chỉ chọn một phương án                                      Nguyễn Quốc Hoàn     0913 661 886

Câu 1. Cho $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên $[1\,\,;\,\,2]$. Khi đó ${\int\limits_{1}^{2}{f(x)dx}}$ bằng

A. ${F(2)-F(1)}$.           B. ${F(2)+F(1)}$.           C. ${F(1)-F(2)}$.           D. ${f(2)-f(1)}$.

Câu 2. Cho $f\left( x \right)$ là một hàm số liên tục và có đạo hàm trên đoạn $\left[ a\,;\,b \right],$ $F\left( x \right)$ là một nguyên hàm của $f\left( x \right)$ trên đoạn $\left[ a\,\,;\,b \right].$ Khi đó ${\int\limits_{a}^{b}{f'(x)dx}}$ bằng

A. ${f\left( a \right)-f\left( b \right)}$.           B. $f\left( b \right)-f\left( a \right)$.           C. $F\left( a \right)-F\left( b \right)$.           D. $F\left( b \right)-F\left( a \right)$.

Câu 3. Cho hàm số bậc ba $y=f\left( x \right)$ có đồ thị là đường cong như hình sau.

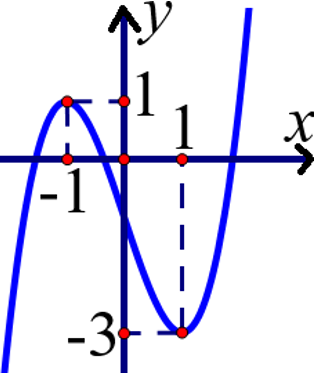Khi đó $\int\limits_{-1}^{1}{f'(x)dx}$ bằng

A. –4.           B. –2.           C. 2.           D. 4.

Câu 4. Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$, biết $f(2)=4.{{\log }_{2}}e$ và $f'(x)={{2}^{x}}+6x$. Khi đó $\int\limits_{0}^{1}{f(x).dx}$ bằng

A. $\dfrac{1}{{{\ln }^{2}}2}-11$.           B. $\dfrac{2}{{{\ln }^{2}}2}-11$.           C. $\dfrac{4}{\ln 2}-4\ln 2-10$.                  D. $\dfrac{4}{\ln 2}-4\ln 2-9$.

Câu 5. $\int\limits_{1}^{4}{\left| x-2 \right|dx}$ bằng

A. $\int\limits_{1}^{2}{\left( x-2 \right)dx+\int\limits_{2}^{4}{\left( x-2 \right)dx}}$.           B. $\int\limits_{1}^{2}{\left( x-2 \right)dx-\int\limits_{2}^{4}{\left( x-2 \right)dx}}$.      

C. $\int\limits_{2}^{4}{\left( x-2 \right)dx-\int\limits_{1}^{2}{\left( x-2 \right)dx}}$.           D. $\int\limits_{1}^{2}{\left( 2-x \right)dx+\int\limits_{2}^{4}{\left( 2-x \right)dx}}$.

Câu 6. Cho hàm số $y=f(x)$ liên tục trên đoạn $[a\,\,;\,\,b]$. Khẳng định nào dưới đây là sai ?

A. $\int\limits_{a}^{b}{f(x)dx=\int\limits_{a}^{b}{f(t)dt.}}$           B. $\int\limits_{a}^{b}{f(x)dx=-\int\limits_{b}^{a}{f(x)dx.}}$

C. $\int\limits_{a}^{b}{kdx=k(a-b),\,\,\forall k\in \mathbb{R}.}$           D. $\int\limits_{a}^{b}{f(x)dx=\int\limits_{a}^{c}{f(x)dx}}+\int\limits_{c}^{b}{f(x)dx,\,\,\forall c\in (a;b).}$

Câu 7. Cho $\int\limits_{0}^{1}{x{{e}^{x}}dx}=1$, khi đó $\int\limits_{0}^{1}{\left( 6x-5 \right).{{e}^{x}}dx}$ bằng

A. $11-5e$.           B. $16-5e$.           C. $5-e$.           D. $7-e$.

Câu 8. Biết $f(x)=4 x^4+2 x-4$ và $F(x)$ là một nguyên hàm của $f(x)$. Khi đó $F(4)-F(1)$ bằng

A. $\dfrac{4108}{5}$.           B. $\dfrac{4107}{5}$.           C. $\dfrac{4104}{5}$.           D. $\dfrac{4106}{5}$.

Câu 9. Biết $\int\limits_{1}^{3}{7f(x)\text{d}x=3},$ $\int\limits_{1}^{3}{9g(y)\text{d}y=-5}$; khi đó $\int\limits_{1}^{3}{\left[ f(x)+g(x) \right]}\,\text{d}x$ bằng

A. $\dfrac{64}{63}$.           B. $\dfrac{-8}{63}$.           C. $\dfrac{62}{63}$.           D. $\dfrac{61}{63}$.

Câu 10. Biết ${\int\limits_{0}^{4}{3f(x)dx}=3}$, ${\int\limits_{0}^{2}{7f(y)dy}=-4}$; khi đó $\int\limits_{2}^{4}{f(z)dz}$ bằng

A. $\dfrac{11}{7}$.           B. $\dfrac{12}{7}$.           C. $\dfrac{9}{7}$.           D. $\dfrac{13}{7}$.

Câu 11. Biết ${\int\limits_{1}^{3}{\left[ 7f(x)+3g(x) \right]dx}\,=5}$, ${\int\limits_{1}^{3}{\left[ 49f(y)+3g(y) \right]dy=-4}}$; khi đó $\int\limits_{1}^{3}{f(z)dz}$ bằng

A. $-\dfrac{5}{14}$.           B. $-\dfrac{2}{7}$.           C. 0.           D. $-\dfrac{3}{14}$.

Câu 12. Giả sử nhiệt độ (tính bằng $^{0}\text{C}$) tại thời điểm $t$ giờ trong khoảng thời gian từ 6 giờ sáng đến 12 giờ trưa ở một địa phương vào một ngày nào đó được mô hình hoá bởi hàm số $T\left( t \right)=20+1,5\left( t-6 \right)$,  $6\le t\le 12$. Nhiệt độ trung bình vào ngày đó trong khoảng thời gian từ 6 giờ sáng đến 12 giờ trưa là

A. $8,{{2}^{0}}$.           B. ${{9}^{0}}$.           C. ${{20}^{0}}$.           D. $24,{{5}^{0}}$.

Phần 2. Trong mỗi ý  a)  b)  c)  d)  ở mỗi câu chỉ chọn đúng hoặc sai        Nguyễn Quốc Hoàn  0913661886

Câu 1. Cho các hàm số $f\left( x \right),\,g\left( x \right)$ liên tục trên đoạn $\left[ -1\,\,;\,\,3 \right]$ thỏa mãn $\int\limits_{-1}^{2}{\left[ 3f\left( x \right)+2g\left( x \right) \right]\text{d}x}=4$, $\int\limits_{-1}^{2}{\left[ 2f\left( x \right)-g\left( x \right) \right]\text{d}x}=5$ và $\int\limits_{-1}^{3}{f\left( x \right)\text{d}x}=6$.

       a) $\int\limits_{-1}^{2}{f\left( x \right)\text{d}x}=2$.

       b) $\int\limits_{-1}^{2}{g\left( x \right)\text{d}x}=1$.

       c) $\int\limits_{2}^{3}{f\left( x \right)\text{d}x}=-4$.

       d) $\int\limits_{2}^{-1}{\left[ x+2f\left( x \right)-3g\left( x \right) \right]\text{d}x}=-\dfrac{3}{2}$.

Câu 2. Một bác thợ bơm nước vào bể chứa nước, biết thể tích bể chứa nước là 2500${{m}^{3}}$. Gọi ${h\left( t \right)}$ là thể tích nước bơm được sau ${t}$ phút. Cho biết ${{h}'\left( t \right)=6a{{t}^{2}}+2bt}$ và ban đầu bể không có nước. Sau 3 phút thì thể tích nước trong bể là ${90{{m}^{3}}}$, sau 6 phút thì thể tích nước trong bể là ${504{{m}^{3}}}$.

       a) ${h\left( t \right)=\int{\left( 6a{{t}^{2}}+2bt \right)\text{d}t}}$.

       b) ${h\left( 3 \right)=\int\limits_{0}^{3}{\left( 6a{{t}^{2}}+2bt \right)\text{d}t=90}}$.

       c) $a,\,\,b$ là nghiệm của hệ phương trình ${\left\{ \begin{align} & 54a+9b=90 \\ & 432a+36b=414 \\ \end{align} \right.}$.

       d) Sau khi bơm 10 phút thì nước đầy bể.

Câu 3. Một công trình xây dựng dự kiến hoàn thành trong 50 ngày. Gọi $M(t)$ là số ngày công được tính đến hết ngày thứ $t$ (kể từ khi khởi công công trình). Trong kinh tế xây dựng, người ta đã biết rằng $M'(t)=m(t)$ với $m(t)$ là số lượng công nhân được sử dụng tại thời điểm $t$. Biết rằng $m(t)=60\,+\,8\sqrt{t}-2t$ (với $0\le t\le 50$).

       a) Có 25 công nhân được sử dụng vào ngày thứ 49.

       b) Số công nhân được sử dụng nhiều nhất vào ngày thứ 4.

       c) Trong 10 ngày đầu tiên, công trình đã cần hơn 650 ngày công.

       d) Phải cần hơn 2350 ngày công để hoàn thành công trình xây dựng đó theo dự kiến.

Câu 4. Một vật chuyển động với vận tốc $v(t)$ được cho bởi đồ thị như hình vẽ sau.

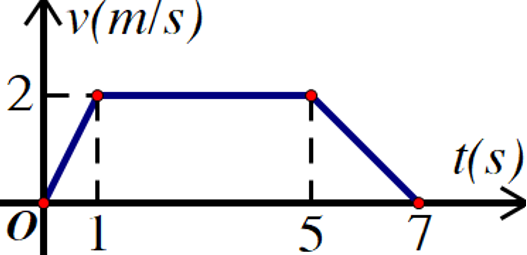      a) Vận tốc của vật tại thời điểm $t=1\,\,(s)$ là $2\,(m/s)$.

      b) Hàm số $v(t)$ được cho bởi công thức $v(t)=\left\{ \begin{align} & 2t,\,\,\,\,\,\,\,\,\,\,\,0\le t<1 \\ & 2,\,\,\,\,\,\,\,\,\,\,\,\,\,1\le t<5 \\  & -t+7,\,\,\,5\le t\le 7 \\ \end{align} \right.$.

       c) Quãng đường vật đi được từ lúc $t=1\,(s)$ đến lúc $t=3\,(s)$ là $2\,m$.

       d) Quãng đường vật đi được trong 6 giây đầu tiên là $10\,m$.

Phần 3. Trả lời các câu hỏi sau                                                           Nguyễn Quốc Hoàn     0913 661 886

Câu 1. Cho ${\int\limits_{1}^{2}{\left( \dfrac{{{x}^{2}}+1}{x} \right)}\,\text{d}x=\ln a+\dfrac{b}{c}}$; biết $a,\,\,b,\,\,c$ là số nguyên. Tính tổng ${a+b+c}$ ?

Câu 2. Tính $\int\limits_{0}^{1}{{{2}^{x}}{{.3}^{x+1}}.dx}$ (làm tròn kết quả đến hàng đơn vị) ?

Câu 3. Tại một khu vực tham quan, gọi $B\left( t \right)$ là hàm số biểu thị số lượng khách tham quan sau $t$ giờ mở cửa, khi đó tốc độ thay đổi lượng khách tham quan trong ngày được biểu diễn bằng hàm số ${{B}'\left( t \right)=4{{t}^{3}}-3{{t}^{2}}+200}$, trong đó t tính bằng giờ (${0\le t\le 8}$), ${{B}'\left( t \right)}$ tính bằng khách/giờ. Sau 2 giờ đã có 1200 người có mặt. Hỏi sau 6 giờ lượng khách tham quan là bao nhiêu người ?

Câu 4. Một quần thể vi khuẩn ban đầu gồm 500 vi khuẩn, sau đó bắt đầu tăng trưởng. Gọi $P\left( t \right)$ là số lượng vi khuẩn của quần thể đó tại thời điểm $t$, trong đó $t$ tính theo ngày $\left( 0\le t\le 10 \right)$. Tốc độ tăng trưởng của quần thể vi khuẩn đó cho bởi hàm số $P'\left( t \right)=k\sqrt{t},$ trong đó $k$ là hằng số. Sau 1 ngày, số lượng vi khuẩn của quần thể đó đã tăng lên thành 600 vi khuẩn. Tính số lượng vi khuẩn của quần thể đó sau 7 ngày (làm tròn kết quả đến hàng đơn vị) ?   (Nguồn: R. Larson and  B. Edwards, Calcucus 10e, Cengage 2014).

Câu 5. Chủ một trung tâm thương mại muốn cho thuê một số gian hàng như nhau. Người đó muốn cho thuê mỗi gian hàng với giá là $x$ triệu đồng $\left( x>0 \right)$. Khi đó doanh thu của cửa hàng được biểu diễn theo hàm số $T\left( x \right)$. Tốc độ thay đổi doanh thu từ các gian hàng đó được biểu diễn bởi hàm số ${T}'\left( x \right)=-10x+200$, trong đó ${T}'\left( x \right)$ tính bằng triệu đồng. Biết rằng nếu giá thuê cho mỗi gian hàng là 10 triệu đồng thì doanh thu là 1800 triệu đồng. Tìm giá trị của ${x}$ để người đó có doanh thu là cao nhất ?

Câu 6. Tại một nhà máy sản xuất gọi ${C\left( x \right)}$ là tổng chi phí tính theo triệu đồng để sản xuất ${x}$ (tấn) sản phẩm A trong một tháng. Khi đó đạo hàm ${{C}'\left( x \right)}$ gọi là chi phí cận biên, cho biết tốc độ tăng tổng chi phí theo lượng sản phẩm được sản xuất. Giả sử chi phí cận biên (tính theo triệu đồng trên tấn) của nhà máy ước lượng bởi công thức ${{C}'\left( x \right)=5-0,06x+0,00072{{x}^{2}}}$ với ${0\le x\le 150}$. Biết rằng ${C\left( 0 \right)=30}$ triệu đồng gọi là chi phí cố định. Tính tổng chi phí khi nhà máy sản xuất 100 tấn sản phẩm A trong một tháng ?

_ _ _ _ _ _ Hết _ _ _ _ _ _

Giáo viên:  Nguyễn Quốc Hoàn  0913661886  (hs.edu.vn)

Thầy cô, Học sinh tải về nếu hỏi mật khẩu thì nhập một trong các mk sau để mở file (NÊN copy và chú ý không dấu cách và không thừa khoảng trắng hay kí tự bất kì):    hs.edu.vn           https://hs.edu.vn/           https://edu365.edu.vn/           https://edu365.edu.vn           edu365.edu.vn           edu365free           freeedu365           edu365.edu.vnfree           edu365 hoc moi luc moi noi

(Nếu file quá nhiều lượt tải về trong ngày, xin bấm vào đây xem hướng dẫn để tải ngay)

Chúng tôi luôn mong nhận được sự đồng hành, góp ý và chia sẻ của thầy cô giáo và học sinh.

Xin gửi về địa chỉ:

Nhà giáo:    Nguyễn Quốc Hoàn

Mobi, Zalo:    0913 661 886

Tel:    025 99 999 888 ,    024 666 07 999 ,    028 99 99 99 77 

Giờ làm việc:    08h11 - 18h36 hàng ngày; trừ các ngày lễ và ngày thứ bẩy, chủ nhật.